Materi, Contoh Soal & Pembahasan Sistem Persamaan Linear Kuadrat (SPLK)
Sistem persamaan yang terdiri atas sebuah persamaan linear dan sebuah persamaan kuadrat yang masing-masing bervariabel dua disebut sistem persamaan linear-kuadrat (SPLK). Berdasarkan karakteristik dari bagian kuadratnya, SPLK dikelompokkan sebagai berikut.
- SPLK dengan bagian kuadrat berbentuk eksplisit.
- SPLK dengan bagian kuadrat berbentuk implisit.
SPLK Dengan Bagian Kuadrat Berbentuk Eksplisit
Bentuk umum SPLK dengan bagian kuadratnya berbentuk eksplisit dapat dituliskan sebagai berikut.
$$\begin{cases} y & = ax + b && (\text{bagian linear}) \\ y & = px^2 + qx + r && (\text{bagian kuadrat}) \end{cases}$$dengan $a, b, p, q, r$ bilangan real dan $a, p \neq 0.$
Sistem ini dapat diselesaikan dengan cara mensubstitusikan persamaan linear ke persamaan kuadrat, kemudian disederhanakan dan diselesaikan dengan menggunakan metode pemfaktoran, melengkapkan kuadrat, atau rumus ABC.
Secara umum, penyelesaian dari SPLK tersebut dapat ditentukan dengan melalui langkah-langkah berikut.
Langkah 1:
Substitusikan bagian linear $y = ax+b$ ke bagian kuadrat $y = px^2+qx+r$, diperoleh
$$\begin{aligned} ax + b & = px^2+qx+r \\ px^2+qx-ax+r-b & = 0 \\ px^2+(q-a)x+(r-b) & = 0 \end{aligned}$$Persamaan terakhir merupakan persamaan kuadrat satu variabel, yaitu $x$. Selesaikan persamaan kuadrat tersebut untuk mencari nilai $x$.
Langkah 2:
Nilai-nilai $x$ yang didapat pada Langkah 1 tadi (jika ada) disubstitusikan ke persamaan $y = ax+b$ (agar perhitungannya lebih mudah), untuk memperoleh nilai $y$. Kita ingat bahwa nilai $x$ yang memenuhi persamaan kuadrat $px^2 + (q-a)x + (r-b) = 0$ disebut akar-akar dari persamaan kuadrat itu. Banyak nilai $x$ (banyak akar) dari persamaan kuadrat tersebut ditentukan oleh nilai diskriminan $D = (q-a)^2-4p(r-b)$. Dengan demikian, banyak anggota dalam himpunan penyelesaian SPLK
$$\begin{cases} y = ax+b \\ y = px^2+qx + r \end{cases}$$ditentukan oleh nilai diskriminan $D$ dengan aturan berikut.
- Jika $D > 0$, maka SPLK tersebut mempunyai dua anggota dalam himpunan penyelesaiannya.
- Jika $D = 0$, maka SPLK tersebut mempunyai satu anggota dalam himpunan penyelesaiannya.
- Jika $D < 0$, maka SPLK tersebut tidak mempunyai anggota dalam himpunan penyelesaiannya. Dengan kata lain, himpunan penyelesaiannya adalah himpunan kosong, dinotasikan $\emptyset$ atau $\{ \}$.
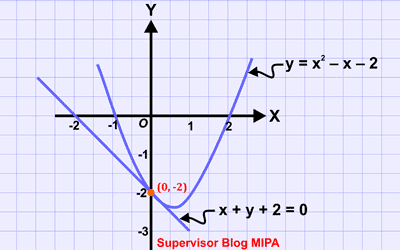
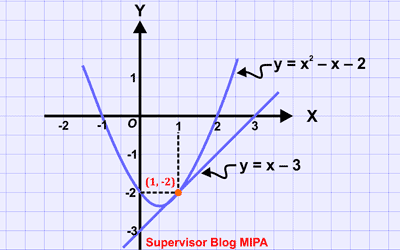
Anggota dari himpunan penyelesaian suatu SPLK dapat ditafsirkan secara geometris sebagai koordinat titik potong antara garis $y = ax+b$ dengan parabola $y = px^2+qx+r$. Kedudukan garis terhadap parabola itu ditentukan oleh nilai diskriminan $D$ dengan aturan berikut.
- Jika $D > 0$, maka garis memotong parabola di dua titik yang berlainan.
- Jika $D = 0$, maka garis memotong parabola tepat di satu titik. Dengan kata lain, garis itu menyinggung parabola.
- Jika $D < 0$, maka garis dan parabola tidak berpotongan.
Perhatikan gambar kedudukan garis $y = ax+b$ dan parabola $y = px^2+qx+r$ berikut agar lebih jelas.

SPLK dengan Bagian Kuadrat Berbentuk Implisit
Persamaan dua variabel $x$ dan $y$ dikatakan berbentuk implisit jika persamaan itu tidak dapat dinyatakan dalam bentuk $y = f(x)$ atau $x = f(y).$ Persamaan implisit dinyatakan dalam bentuk $f(x, y) = 0.$
Contoh persamaan dua variabel dalam bentuk implisit adalah sebagai berikut.
a. $x^2+y^2+8 = 0$
b. $x^2+2y^2-3x+y = 0$
c. $x^2-y^2-3x+4y+9 = 0$
d. $2x^2+xy+y^2+3y-4 = 0$
Secara umum, SPLK dengan bagian kuadratnya berbentuk implisit dapat dituliskan sebagai berikut.
$$\begin{cases} px+qy + r = 0 & (\text{bagian linear}) \\ ax^2+by^2 + cxy + dx + ey + f = 0 & (\text{bagian kuadrat berbentuk implisit}) \end{cases}$$dengan $a, b, c, d, e, f, p, q, r$ semuanya merupakan bilangan real dan $p, q, a, b \neq 0.$ SPLK dengan bagian kuadrat berbentuk implisit dibagi menjadi dua, yaitu bentuk implisit yang tak dapat difaktorkan dan bentuk implisit yang dapat difaktorkan.
Berikut ini disajikan beberapa soal mengenai sistem persamaan linear dan kuadrat, disertai dengan pembahasannya.
Bagian Pilihan Ganda
Soal Nomor 1
Penyelesaian dari sistem persamaan $$\begin{cases} y & = 3x-5 && (\cdots 1) \\ y & = x^2-5x+7 && (\cdots 2) \end{cases}$$adalah $\cdots \cdot$
A. $(-2, 1)$ dan $(6, 13)$
B. $(-2, -1)$ dan $(6, -13)$
C. $(2, -1)$ dan $(-6, 13)$
D. $(2, 1)$ dan $(6, 13)$
E. $(2, 1)$ dan $(-6, -13)$
Pertama, cari titik potong dari grafik kedua persamaan tersebut.
$$\begin{aligned} y & = y \\ x^2-5x+7 & = 3x-5 \\ x^2-8x+12 & = 0 \\ (x-6)(x-2) & = 0 \\ x = 6~\text{atau}~x & = 2 \end{aligned}$$Substitusi nilai $x$ ke persamaan $(1)$, yaitu $y = 3\color{red}{x}-5$.
$$\begin{aligned} x = \color{blue}{6} & \Rightarrow y = 3(6)-5 = \color{blue}{13} \\ x = \color{green}{2} & \Rightarrow y = 3(2)-5 = \color{green}{1} \end{aligned}$$Jadi, penyelesaian sistem persamaan linear-kuadrat tersebut adalah $(6, 13)$ dan $(2, 1)$.
(Jawaban D)
Soal Nomor 2
Himpunan penyelesaian dari SPLK $\begin{cases} x+y = 0 \\ x^2+y^2+8 = 0 \end{cases}$ adalah $\cdots \cdot$
A. $\{(2, -2), (-2, 2)\}$
B. $\{(-2, -2), (2, 2)\}$
C. $\{(4, -4), (-4, 4)\}$
D. $\{(2, -4), (-4, 4)\}$
E. $\{(2, 2), (4, 4)\}$
Diketahui SPLK
$$\begin{cases} x+y = 0 & (\cdots 1) \\ x^2+y^2-8 = 0 & (\cdots 2) \end{cases}$$Persamaan $(1)$ dapat ditulis menjadi $y = -x$. Substitusikan pada persamaan $(2)$.
$$\begin{aligned} x^2+\color{red}{y}^2-8 & = 0 \\ x^2+(-x)^2-8 & = 0 \\ x^2+x^2 & = 8 \\ 2x^2 & = 8 \\ x^2 & = 4 \\ x & = \pm 2 \end{aligned}$$Jika $x = 2$, maka diperoleh $y = -2$.
Jika $x = -2$, maka diperoleh $y = 2$.
Jadi, HP SPLK tersebut adalah $\boxed{\{(2, -2), (-2, 2)\}}$
(Jawaban A)
Soal Nomor 3
Misalkan penyelesaian SPLK $\begin{cases} x-y+1 = 0 \\ x^2+y^2-13 = 0 \end{cases}$ adalah $(a, b)$ dan $(c, d)$. Nilai $a+b+c+d = \cdots \cdot$
A. $-3$ C. $0$ E. $12$
B. $-2$ D. $3$
Diketahui SPLK
$$\begin{cases} x-y+1 = 0 & (\cdots 1) \\ x^2+y^2-13 = 0 & (\cdots 2) \end{cases}$$Persamaan $(1)$ dapat ditulis menjadi $y = x+1$. Substitusikan pada persamaan $(2)$.
$$\begin{aligned} x^2+\color{red}{y}^2-13 & = 0 \\ x^2+(x+1)^2-13 & = 0 \\ x^2+(x^2+2x+1)-13 & = 0 \\ 2x^2+2x-12 & = 0 \\ x^2+x-6 & = 0 \\ (x+3)(x-2) & = 0 \\ x = -3~\text{atau}~x & = 2 \end{aligned}$$Jika $x = -3$, maka diperoleh $y = -2$.
Jika $x = 2$, maka diperoleh $y = 3$.
Jadi, penyelesaian SPLK tersebut adalah $(-3, -2)$ dan $(2, 3)$ sehingga nilai $$\boxed{a+b+c+d = -3+(-2)+2+3 = 0}$$Catatan: Karena yang ditanyakan adalah jumlah dari $a, b, c, d$, maka masing-masing nilainya tidak perlu dipermasalahkan bila ditukar-tukar, sebab hasil penjumlahannya pasti sama.
(Jawaban C)
Soal Nomor 4
Titik koordinat yang termasuk penyelesaian dari sistem persamaan $\begin{cases} y & = 2x+5 \\ y & = x^2-3 \end{cases}$ adalah $\cdots \cdot$
A. $(-4, 13)$ D. $(2, -1)$
B. $(-2, 1)$ E. $(4, 11)$
C. $(0, -4)$
Pertama, cari titik potong dari grafik kedua persamaan tersebut.
$$\begin{aligned} y & = y \\ x^2-3 & = 2x+5 \\ x^2-2x-8 & = 0 \\ (x-4)(x+2) & = 0 \\ x = 4~\text{atau}~x & = -2 \end{aligned}$$Substitusi masing-masing dua nilai $x$ tersebut ke persamaan $y = 2x+5$ sehingga diperoleh
$$\begin{aligned} x = 4 & \Rightarrow y = 2(4) + 5 = 13 \\ x = -2 & \Rightarrow y = 2(-2) + 5 = 1 \end{aligned}$$Jadi, titik potongnya adalah $(4, 13)$ dan $(-2, 1)$.
Titik potong adalah titik koordinat yang merupakan penyelesaian dari sistem persamaan tersebut.
(Jawaban B)
Penyelesaian dari sistem persamaan
$$\begin{cases} x-y = 2 & (\cdots 1) \\ x^2+16y^2-24xy-16 = 0 & (\cdots 2) \end{cases}$$adalah $\cdots \cdot$
A. $(6, 4)$ dan $\left(\dfrac{12}{7}, -\dfrac{2}{7}\right)$
B. $(6, 4)$ dan $\left(\dfrac{2}{7}, -\dfrac{12}{7}\right)$
C. $(-4, -6)$ dan $\left(\dfrac{2}{7}, -\dfrac{12}{7}\right)$
D. $(-4, -6)$ dan $\left(\dfrac{12}{7}, -\dfrac{2}{7}\right)$
E. $(-4, -6)$ dan $(6, 4)$
Ubah persamaan $(1)$ menjadi
$$x = 2 + y~~~~(\cdots 3)$$Substitusi persamaan $(3)$ pada persamaan $(2)$. Kita peroleh
$$\begin{aligned} \color{blue}{x}^2+16y^2-24\color{blue}{x}y-16 = 0 \\ (2+y)^2+16y^2-24(2+y)y-16 & = 0 \\ y^2+4y+4+16y^2-48y-24y^2-16 & = 0 \\ -7y^2-44y-12 & = 0 \\ 7y^2+44y+12 & = 0 \\ (7y+2)(y+6) & = 0 \\ y = -\dfrac27~\text{atau}~y & = -6 \end{aligned}$$Substitusi nilai $y$ ke persamaan $(1)$, yaitu $x = 2+\color{red}{y}$.
$$\begin{aligned} y = \color{blue}{-\dfrac27} & \Rightarrow x = 2+\color{blue}{-\dfrac27} = \dfrac{12}{7} \\ y = \color{green}{-6} & \Rightarrow x = 2+\color{red}(-6) = -4 \end{aligned}$$Jadi, penyelesaian sistem persamaan linear-kuadrat tersebut adalah $(-4, -6)$ dan $\left(\dfrac{12}{7}, -\dfrac27\right)$.
(Jawaban D)
Himpunan penyelesaian SPLK $$\begin{cases} 2x+3y = 8 \\ 4x^2-12xy+9y^2 = 16 \end{cases}$$adalah $\cdots \cdot$
A. $\left\{(1, 2), \left(3, \dfrac23\right)\right\}$
B. $\left\{(2, 1), \left(3, \dfrac23\right)\right\}$
C. $\left\{(1, 2), \left(\dfrac23, 3\right)\right\}$
D. $\left\{(2, 1), \left(\dfrac23, 3\right)\right\}$
E. $\emptyset$
Diketahui SPLK
$$\begin{cases} 2x+3y = 8 & (\cdots 1) \\ 4x^2-12xy+9y^2 = 16 & (\cdots 2) \end{cases}$$Persamaan $(2)$ merupakan bagian kuadrat yang dapat difaktorkan sebagai berikut.
$$\begin{aligned} 4x^2-12xy+9y^2 & = 16 \\ (2x-3y)^2 & = 16 \\ (2x-3y)^2-4^2 & = 0 \\ (2x-3y+4)(2x-3y-4) & = 0 \\ 2x-3y+4 = 0~\text{atau}~2x-3y&-4 = 0 \end{aligned}$$Dengan demikian, SPLK tersebut dapat dipecah menjadi dua SPLDV berikut.
SPLDV pertama:
$$\begin{cases} 2x+3y & = 8 \\ 2x-3y + 4 & = 0 \end{cases}$$dengan penyelesaian $(1, 2)$.
SPLDV kedua:
$$\begin{cases} 2x+3y & = 8 \\ 2x-3y-4 & = 0 \end{cases}$$dengan penyelesaian $\left(3, \dfrac23\right)$.
Jadi, himpunan penyelesaian SPLK tersebut adalah $\boxed{\left\{(1, 2), \left(3, \dfrac23\right)\right\}}$
(Jawaban A)
Essay
Soal Nomor 1
Carilah himpunan penyelesaian dari tiap SPLK berikut.
a. $\begin{cases} y & = 6-5x \\ y & = x^2 \end{cases}$
b. $\begin{cases} y & = x+3 \\ y & = x^2-5x+8 \end{cases}$
c. $\begin{cases} y & = 3x-8 \\ y & = x^2-3x \end{cases}$
d. $\begin{cases} y & = x+1 \\ y & = x^2+x \end{cases}$
Jawaban a)
Diketahui
$$\begin{cases} y & = 6-5x && (\cdots 1) \\ y & = x^2 && (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$ sehingga diperoleh
$$\begin{aligned} x^2 & = 6-5x \\ x^2+5x-6 & = 0 \\ (x+6)(x-1) & = 0 \\ x = -6~\text{atau}~x & = 1 \end{aligned}$$Dengan demikian, kita akan dapatkan nilai $y$ jika masing-masing nilai $x$ ini disubstitusi pada salah satu persamaan, misalnya $y = x^2$.
$$\begin{aligned} x = -6 & \Rightarrow y = (-6)^2 = 36 \\ x = 1 & \Rightarrow y = (1)^2 = 1 \end{aligned}$$Jadi, HP SPLK tersebut adalah $\boxed{\{(-6, 36), (1, 1)\}}$
Jawaban b)
Diketahui
$$\begin{cases} y & = x+3 && (\cdots 1) \\ y & = x^2-5x+8 && (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$sehingga diperoleh
$$\begin{aligned} x^2-5x+8 & = x+3 \\ x^2-6x+5 & = 0 \\ (x-5)(x-1) & = 0 \\ x = 5~\text{atau}~x & = 1 \end{aligned}$$Dengan demikian, kita akan dapatkan nilai $y$ jika masing-masing nilai $x$ ini disubstitusi pada salah satu persamaan, misalnya $y = x+3$.
$$\begin{aligned} x = 5 & \Rightarrow y = 5+3 = 8 \\ x = 1 & \Rightarrow y = 1+3 = 4 \end{aligned}$$Jadi, HP SPLK tersebut adalah $\boxed{\{(5, 8), (1, 4)\}}$
Jawaban c)
Diketahui
$$\begin{cases} y & = 3x-8 && (\cdots 1) \\ y & = x^2-3x && (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$ sehingga diperoleh
$$\begin{aligned} x^2-3x & = 3x-8 \\ x^2-6x+8 & = 0 \\ (x-2)(x-4) & = 0 \\ x = 2~\text{atau}~x & = 4 \end{aligned}$$Dengan demikian, kita akan dapatkan nilai $y$ jika masing-masing nilai $x$ ini disubstitusi pada salah satu persamaan, misalnya $y = 3x-8$.
$$\begin{aligned} x = 2 & \Rightarrow y = 3(2)-8 = -2 \\ x = 4 & \Rightarrow y = 3(4)-8 = 4 \end{aligned}$$Jadi, HP SPLK tersebut adalah $\boxed{\{(2, -2), (4, 4)\}}$
Jawaban d)
Diketahui
$$\begin{cases} y & = x+1 && (\cdots 1) \\ y & = x^2+x && (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$ sehingga diperoleh
$$\begin{aligned} x^2+x & = x+1 \\ x^2-1 & = 0 \\ (x+1)(x-1) & = 0 \\ x = -1~\text{atau}~x & = 1 \end{aligned}$$Dengan demikian, kita akan dapatkan nilai $y$ jika masing-masing nilai $x$ ini disubstitusi pada salah satu persamaan, misalnya $y = x+1$.
$$\begin{aligned} x = -1 & \Rightarrow y = -1+1 = 0 \\ x = 1 & \Rightarrow y = 1+1 = 2 \end{aligned}$$Jadi, HP SPLK tersebut adalah $\boxed{\{(-1, 0), (1, 2)\}}$
Soal Nomor 2
Diketahui SPLK 2
$$\begin{cases} 2x+y+1 & = 0 \\ y & = x^2-4x \end{cases}$$
- Tunjukkan bahwa sistem persamaan linear dan kuadrat itu tepat memiliki satu anggota dalam himpunan penyelesaiannya.
- Carilah himpunan penyelesaiannya itu.
Jawaban a)
Diketahui
$$\begin{cases} 2x+y+1 & = 0 && (\cdots 1) \\ y & = x^2-4x && (\cdots 2) \end{cases}$$Persamaan $(1)$ dapat diubah menjadi $y = -2x-1$.
Substitusikan persamaan ini ke persamaan $(2)$ sehingga diperoleh
$$\begin{aligned} -2x-1 & = x^2-4x \\ 0 & = x^2-2x+1 \end{aligned}$$Sistem tersebut memiliki tepat satu penyelesaian jika persamaan kuadrat di atas memiliki diskriminan yang nilainya $0$.
$$\begin{aligned} D & = b^2-4ac \\ & = (-2)^2-4(1)(1) \\ & = 4-4 = 0 \end{aligned}$$(Terbukti)
Jawaban b)
Sebelumnya, kita peroleh persamaan kuadrat $x^2-2x+1 = 0$, yang dapat difaktorkan menjadi $(x-1)^2 = 0$ sehingga penyelesaiannya adalah $x=1$.
Substitusi $x=1$ pada persamaan linearnya sehingga didapat
$$y = -2\color{red}{x}-1 = -2(1)-1 = -3 $$Jadi, penyelesaian SPLK tersebut adalah $\boxed{\{(1, -3)\}}$
Soal Nomor 3
Carilah nilai $a$ agar tiap SPLK berikut ini tepat mempunyai satu anggota dalam himpunan penyelesaiannya.
a. $\begin{cases} y & = x+a \\ y & = x^2-3x \end{cases}$
b. $\begin{cases} y & = ax+1 \\ y & = \dfrac12x^2+x+1 \end{cases}$
c. $\begin{cases} y & = x+a \\ y & = \dfrac12x^2-2 \end{cases}$
d. $\begin{cases} y & = ax+2 \\ y & = ax^2+x+1 \end{cases}$
Jawaban a)
Diketahui
$$\begin{cases} y & = x+a && (\cdots 1) \\ y & = x^2-3x && (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$ sehingga diperoleh
$$\begin{aligned} x^2-3x & = x+a \\ \underbrace{1}_{\color{red}{a}}x^2\underbrace{-4}_{b}x+\underbrace{(-a)}_{c} & = 0 \end{aligned}$$SPLK tersebut akan memiliki tepat satu penyelesaian apabila nilai diskriminan $D$ persamaan kuadrat di atas bernilai $0$.
$$\begin{aligned} D & = 0 \\ b^2-4\color{red}{a}c & = 0 \\ (-4)^2-4(1)(-a) & = 0 \\ 16+4a & = 0 \\ 4a & = -16 \\ a & = -4 \end{aligned}$$Jadi, nilai $a$ yang memenuhi adalah $\boxed{a=-4}$
Jawaban b)
Diketahui
$$\begin{cases} y & = ax+1 && (\cdots 1) \\ y & = \dfrac12x^2+x+1 && (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$ sehingga diperoleh
$$\begin{aligned} \dfrac12x^2+x+1 & = ax+1 \\ \underbrace{\dfrac12}_{\color{red}{a}}x^2+\underbrace{(1-a)}_{b}x+\underbrace{0}_{c} & = 0 \end{aligned}$$SPLK tersebut akan memiliki tepat satu penyelesaian apabila nilai diskriminan $D$ persamaan kuadrat di atas bernilai $0$.
$$\begin{aligned} D & = 0 \\ b^2-4\color{red}{a}c & = 0 \\ (1-a)^2-4\left(\dfrac12\right)(0) & = 0 \\ (1-a)^2 & = 0 \\ 1-a & = 0 \\ a & = 1 \end{aligned}$$Jadi, nilai $a$ yang memenuhi adalah $\boxed{a=1}$
Jawaban c)
Diketahui
$$\begin{cases} y & = x+a && (\cdots 1) \\ y & = \dfrac12x^2-2 && (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$ sehingga diperoleh
$$\begin{aligned} \dfrac12x^2-2 & = x+a \\ \underbrace{\dfrac12}_{\color{red}{a}}x^2\underbrace{-1}_{b}x+\underbrace{(-2-a)}_{c} & = 0 \end{aligned}$$SPLK tersebut akan memiliki tepat satu penyelesaian apabila nilai diskriminan $D$ persamaan kuadrat di atas bernilai $0$.
$$\begin{aligned} D & = 0 \\ b^2-4\color{red}{a}c & = 0 \\ (-1)^2-4\left(\dfrac12\right)(-2-a) & = 0 \\ 1+4+2a & = 0 \\ 2a & = -5 \\ a & = -\dfrac52 \end{aligned}$$Jadi, nilai $a$ yang memenuhi adalah $\boxed{a=-\dfrac52}$
Jawaban d)
Diketahui
$$\begin{cases} y & = ax+2 && (\cdots 1) \\ y & = ax^2+x+1 && (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$ sehingga diperoleh
$$\begin{aligned} ax^2+x+1 & = ax+2 \\ \underbrace{a}_{\color{red}{a}}x^2+\underbrace{(1-a)}_{b}x+\underbrace{(-1)}_{c} & = 0 \end{aligned}$$SPLK tersebut akan memiliki tepat satu penyelesaian apabila nilai diskriminan $D$ persamaan kuadrat di atas bernilai $0$.
$$\begin{aligned} D & = 0 \\ b^2-4\color{red}{a}c & = 0 \\ (1-a)^2-4(a)(-1) & = 0 \\ (1-2a+a^2)+4a & = 0 \\ a^2+2a+1 & = 0 \\ (a+1)^2 & = 0 \\ a & = -1 \end{aligned}$$Jadi, nilai $a$ yang memenuhi adalah $\boxed{a=-1}$
Soal Nomor 4
Carilah batas-batas nilai $a$ agar setiap SPLK berikut ini sekurang-kurangnya memiliki satu anggota himpunan penyelesaian.
a. $\begin{cases} y & = 2x+a \\ y & = x^2-4x+5 \end{cases}$
b. $\begin{cases} 3x+y & = -1 \\ y^2-2ax & = 0 \end{cases}$
Jawaban a)
Diketahui $$\begin{cases} y & = 2x+a && (\cdots 1) \\ y & = x^2-4x+5 && (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$ sehingga diperoleh
$$\begin{cases} x^2-4x+5 & = 2x+a \\ \underbrace{1}_{\color{red}{a}}x^2\underbrace{-6}_{b}x+\underbrace{(5-a)}_{c} & = 0 \end{cases}$$SPLK tersebut akan memiliki setidaknya satu penyelesaian jika persamaan kuadrat di atas memiliki nilai diskriminan $D \geq 0$.
Dengan demikian, kita tuliskan
$$\begin{aligned} D & \geq 0 \\ b^2-4\color{red}{a}c & \geq 0 \\ (-6)^2-4(1)(5-a) & \geq 0 \\ 36-20+4a & \geq 0 \\ 16+4a & \geq 0 \\ 4a & \geq -16 \\ a & \geq -4 \end{aligned}$$Jadi, batas nilai $a$ agar SPLK ini memiliki sekurang-kurangnya satu anggota himpunan penyelesaian adalah $\boxed{a \geq -4}$
Jawaban b)
Diketahui $$\begin{cases} 3x+y & = -1 && (\cdots 1) \\ y^2-2ax & = 0 && (\cdots 2) \end{cases}$$Persamaan $(1)$ dapat ditulis menjadi $y = -1-3x$.
Substitusikan persamaan ini pada persamaan $(2)$ sehingga diperoleh
$$\begin{cases} (-1-3x)^2-2ax & = 0 \\ (1+6x+9x^2)-2ax & = 0 \\ \underbrace{9}_{\color{red}{a}}x^2+\underbrace{(6-2a)}_{b}x+\underbrace{1}_{c} & = 0 \end{cases}$$SPLK tersebut akan memiliki setidaknya satu penyelesaian jika persamaan kuadrat di atas memiliki nilai diskriminan $D \geq 0$.
Dengan demikian, kita tuliskan
$$\begin{aligned} D & \geq 0 \\ b^2-4\color{red}{a}c & \geq 0 \\ (6-2a)^2-4(9)(1) & \geq 0 \\ 4(3-a)^2-4(9) & \geq 0 \\ (3-a)^2-9 & \geq 0 && (\text{bagi}~4) \\ (3-a)^2 & \geq 9 \\ 3-a \leq -3~\text{atau}~& 3-a \geq 3 \\ -a \leq -6~\text{atau}~& -a \geq 0 \\ a \geq 6~\text{atau}~& a \leq 0 \end{aligned}$$Jadi, batas nilai $a$ agar SPLK ini memiliki sekurang-kurangnya satu anggota himpunan penyelesaian adalah $\boxed{a \leq 0~\text{atau}~a \geq 6}$
Carilah nilai $m$ agar tiap SPLK berikut tepat mempunyai satu anggota dalam himpunan penyelesaiannya.
a. $\begin{cases} y = x+m \\ x^2+4y^2-4 = 0 \end{cases}$
b. $\begin{cases} y = mx \\ x^2+y^2-8x-4y+16 = 0 \end{cases}$
Jawaban a)
Diketahui
$$\begin{cases} y = x+m & (\cdots 1) \\ x^2 + 4y^2-4 = 0 & (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$ sehingga diperoleh
$$\begin{aligned} x^2+4(x+m)^2-4 & = 0 \\ x^2+4(x^2+2mx+m^2)-4 & = 0 \\ 5x^2+8mx+(4m^2-4) & = 0 \end{aligned}$$SPLK tersebut akan memiliki tepat satu penyelesaian apabila persamaan kuadrat di atas memiliki nilai diskriminan sama dengan $0$. Kita peroleh
$$\begin{aligned} D & = 0 \\ b^2-4ac & = 0 \\ (8m)^2-4(5)(4m^2-4) & = 0 \\ 64m^2-80m^2+80 & = 0 \\ -16m^2 + 80 & = 0 \\ -m^2 + 5 & = 0 && (\text{bagi}~16) \\ m^2 & = 5 \\ m & = \pm \sqrt5 \end{aligned}$$Jadi, nilai $m$ yang memuat SPLK tersebut memiliki tepat satu penyelesaian adalah $m = \sqrt5$ atau $m = -\sqrt5$.
Jawaban b)
Diketahui
$$\begin{cases} y = mx & (\cdots 1) \\ x^2 +y^2-8x-4y+16 = 0 & (\cdots 2) \end{cases}$$Substitusikan persamaan $(1)$ pada persamaan $(2)$ sehingga diperoleh
$$\begin{aligned} x^2+(mx)^2-8x-4(mx)+16 & = 0 \\ (1+m^2)x^2+(-8-4m)x+16 & = 0 \end{aligned}$$SPLK tersebut akan memiliki tepat satu penyelesaian apabila persamaan kuadrat di atas memiliki nilai diskriminan sama dengan $0$. Kita peroleh
$$\begin{aligned} D & = 0 \\ b^2-4ac & = 0 \\ (-8-4m)^2-4(1+m^2)(16) & = 0 \\ 16(2+m)^2-4(1+m^2)(16) & = 0 \\ (2+m)^2-4(1+m^2) & = 0 && (\text{bagi}~16) \\ 4+4m+m^2-4-4m^2 & = 0 \\ -3m^2+4m & = 0 \\ m(-3m + 4) & = 0 \\ m = 0~\text{atau}~m & = \dfrac43 \end{aligned}$$Jadi, nilai $m$ yang memuat SPLK tersebut memiliki tepat satu penyelesaian adalah $m = 0$ atau $m = \dfrac43$.
Soal Nomor 6
Misalkan $p, q$ adalah bilangan real yang bukan nol. Carilah himpunan penyelesaian dari SPLK berikut ini dengan menyatakannya dalam $p$ dan $q$.
a. $\begin{cases} px + qy = 0 \\ p^2x^2 + pqx + q^2y^2 = 0 \end{cases}$
b. $\begin{cases} x+y = p+q \\ x^2+y^2+xy-p^2-q^2-pq = 0 \end{cases}$
Jawaban a)
Diketahui
$$\begin{cases} px + qy = 0 & (\cdots 1) \\ p^2x^2 + pqx + q^2y^2 = 0 & (\cdots 2) \end{cases}$$Persamaan $(1)$ dapat ditulis kembali menjadi $y = -\dfrac{px}{q}$. Substitusikan pada persamaan $(2)$.
$$\begin{aligned} p^2x^2 + pqx + q^2\color{red}{y}^2 & = 0 \\ p^2x^2 + pqx + q^2\left(-\dfrac{px}{q}\right)^2 & = 0 \\ p^2x^2 + pqx + \cancel{q^2} \cdot \dfrac{p^2x^2}{\cancel{q^2}} & = 0 \\ 2p^2x^2 + pqx & = 0 \\ px(2px + q) & = 0 \end{aligned}$$Persamaan terakhir menunjukkan bahwa kita telah memperoleh
$$\begin{aligned} px = 0 & \Rightarrow x = 0 \\ 2px + q = 0 & \Rightarrow x = -\dfrac{q}{2p} \end{aligned}$$Masing-masing nilai $x$ ini disubstitusi pada persamaan $y = -\dfrac{px}{q}$. Kita akan memperoleh
$$\begin{aligned} x = 0 & \Rightarrow y = -\dfrac{p(0)}{q} = 0 \\ x = -\dfrac{q}{2p} & \Rightarrow y = -\dfrac{p}{q} \cdot \left(-\dfrac{q}{2p}\right) = \dfrac12 \end{aligned}$$Jadi, himpunan penyelesaian SPLK tersebut adalah $$\boxed{\left\{(0, 0), \left(-\dfrac{q}{2p}, \dfrac12\right)\right\}}$$Jawaban b)
Diketahui
$$\begin{cases} x+y = p+q & (\cdots 1) \\ x^2+y^2+xy-p^2-q^2-pq = 0 & (\cdots 2) \end{cases}$$Kedua ruas pada persamaan $(1)$ dikuadratkan, dan kita akan peroleh
$$\begin{aligned} (x+y)^2 & = (p+q)^2 \\ x^2+2xy+y^2 & = p^2+2pq+q^2 \\ x^2+y^2+2xy-p^2-q^2-2pq & = 0 && (\cdots 3) \end{aligned}$$Sekarang, persamaan $(3)$ dikurangi persamaan $(2)$.
$$\begin{aligned} \! \begin{aligned} x^2+y^2+2xy-p^2-q^2-2pq & = 0 \\ x^2+y^2+xy-p^2-q^2-pq & = 0 \end{aligned} \\ \rule{7 cm}{0.6pt} – \\ \! \begin{aligned} xy-pq & = 0 \\ xy & = pq \end{aligned} \end{aligned}$$Dengan demikian, kita dapat tuliskan
$$\begin{cases} x+y & = p+q && (\cdots 1) \\ xy & = pq && (\cdots 2) \end{cases}$$Dengan demikian, didapat dua penyelesaian, yaitu $(x, y) = (p, q)$ atau $(x, y) = (q, p)$.
Jadi, himpunan penyelesaian SPLK tersebut adalah $$\boxed{\{(p, q), (q, p)\}}$$
Soal Nomor 7
Tentukan himpunan penyelesaian SPLK berikut.
a. $\begin{cases} y = x + 1 \\ x^2+y^2-25 = 0 \end{cases}$
b. $\begin{cases} 2x-y-3 = 0 \\ x^2-y^2 = 0 \end{cases}$
c. $\begin{cases} 3x-y-16 = 0 \\ x^2+y^2-6x+4y-12 = 0 \end{cases}$
Jawaban a)
Diketahui SPLK
$$\begin{cases} y = x + 1 & (\cdots 1) \\ x^2+y^2-25 = 0 & (\cdots 2) \end{cases}$$Persamaan $(1)$ disubstitusikan pada persamaan $(2)$.
$$\begin{aligned} x^2+\color{red}{y}^2-25 & = 0 \\ x^2+(x+1)^2-25 & = 0 \\ x^2+(x^2+2x+1)-25 & = 0 \\ 2x^2 +2x-24 & = 0 \\ x^2+x-12 & = 0 \\ (x+4)(x-3) & = 0 \\ x = -4~\text{atau}~x & = 3 \end{aligned}$$Jika $x = -4$, maka diperoleh $y = -3$.
Jika $x = 3$, maka diperoleh $y = 4$.
Jadi, HP SPLK tersebut adalah $\boxed{\{(-4, -3), (3, 4)\}}$
Jawaban b)
Diketahui SPLK
$$\begin{cases} 2x-y-3 = 0 & (\cdots 1) \\ x^2-y^2 = 0 & (\cdots 2) \end{cases}$$Persamaan $(1)$ dapat ditulis menjadi $y = 2x-3$. Substitusikan pada persamaan $(2)$.
$$\begin{aligned} x^2-\color{red}{y}^2 & = 0 \\ (x+\color{red}{y})(x-\color{red}{y}) & = 0 \\ (x+(2x-3))(x-(2x-3)) & = 0 \\ (3x-3)(-x+3) & = 0 \\ x = 1~\text{atau}~x & = 3 \end{aligned}$$Jika $x = 1$, maka diperoleh $y = -1$.
Jika $x = 3$, maka diperoleh $y = 3$.
Jadi, HP SPLK tersebut adalah $\boxed{\{(1, -1), (3, 3)\}}$
Jawaban c)
Diketahui SPLK
$$\begin{cases} 3x-y-16 = 0 & (\cdots 1) \\ x^2+y^2-6x+4y-12 = 0 & (\cdots 2) \end{cases}$$Persamaan $(1)$ dapat ditulis menjadi $y = 3x-16$. Substitusikan pada persamaan $(2)$.
$$\begin{aligned} x^2+\color{red}{y}^2-6x+4\color{red}{y}-12 & = 0 \\ x^2 + (3x-16)^2-6x + 4(3x-16)-12 & = 0 \\ x^2 + (9x^2-96x+256)-6x + 12x-64-12 & = 0 \\ 10x^2-90x+180 & = 0 \\ x^2-9x+18 & = 0 && (\text{bagi}~10) \\ (x-3)(x-6) & = 0 \end{aligned}$$Jika $x = 3$, maka diperoleh $y = -7$.
Jika $x = 6$, maka diperoleh $y = 2$.
Jadi, HP SPLK tersebut adalah $\boxed{\{3, -7), (6, 2)\}}$
1. Soal EBTANAS Matematika IPA SMA 1995
Himpunan penyelesaian sistem persamaan
$\left\{\begin{matrix}
x-y =1 \\
x^{2}-6x-y+5=0
\end{matrix}\right.$
adalah $\left \{\left ( x_{1},y_{1} \right ),\left ( x_{2},y_{2} \right ) \right \}$
Nilai $x_{1}+x_{2}=\cdots$
$\begin{align}
(A)\ & 1 \\
(B)\ & 5 \\
(C)\ & 6 \\
(D)\ & 7 \\
(E)\ & 11
\end{align}$
Show
Langkah pertama kita subsitusi nilai $y$ pada persamaan linear dan $y$ persamaan kuadrat, dapat kita tuliskan:
$\begin{align}
y &= y \\
x^{2}-6x +5 & = x-1 \\
x^{2}-6x-x +5+1 & = 0 \\
x^{2}-7x + 6 & = 0 \\
\left(x-6 \right)\left(x-1 \right) &= 0 \\
x=6\ \text{atau}\ x=1 & \\
\end{align}$
Yang ditanyakan pada soal adalah $x_{1}+x_{2}=1+6=7$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 7$
Jika kita teruskan untuk mencari himpunan penyelesaian sistem persamaan di atas, langkah berikutnya adalah:
- untuk $x=1$ maka $y=x-1=0$ kita peroleh titik potong $(1,0)$
- untuk $x=6$ maka $y=x-1=5$ kita peroleh titik potong $(6,5)$
- Himpunan Penyelesaian adalah $\left\{ \left(1,0 \right),\ \left(6,5 \right) \right\}$
2. Soal EBTANAS Matematika IPA SMA 1990
Parabola dengan persamaan $y = – x^{2} + 3x + 11$ dan garis dengan persamaan $y – 2x + 1 = 0$ berpotongan di titik yang berabsis...
$\begin{align}
(A)\ & -3\ \text{dan}\ 4 \\
(B)\ & -2\ \text{dan}\ 5 \\
(C)\ & -2\ \text{dan}\ 1 \\
(D)\ & -4\ \text{dan}\ 3 \\
(E)\ & -7\ \text{dan}\ 7 \\
\end{align}$
Show
Langkah pertama kita subsitusi nilai $y$ pada persamaan linear dan $y$ persamaan kuadrat, dapat kita tuliskan:
$\begin{align}
y &= y \\
– x^{2} + 3x + 11 & = 2x - 1 \\
-x^{2}+3x-2x +11+1 & = 0 \\
-x^{2}+ x +12 & = 0 \\
x^{2}- x -12 & = 0 \\
\left(x-4 \right)\left(x+3 \right) &= 0 \\
x=4\ \text{atau}\ x=-3 & \\
\end{align}$
Yang ditanyakan pada soal nilai absis titik potong yaitu $x_{1}=4$ $x_{2}=-3$
$\therefore$ Pilihan yang sesuai adalah $(A)\ -3\ \text{dan}\ 4$
Jika kita teruskan untuk mencari himpunan penyelesaian sistem persamaan di atas, langkah berikutnya adalah:
- untuk $x=-3$ maka $y=2x-1=-7$ kita peroleh titik potong $(-3,-7)$
- untuk $x=4$ maka $y=2x-1=7$ kita peroleh titik potong $(4,7)$
- Himpunan Penyelesaian adalah $\left\{\left(-3,-7 \right),\ \left(4,7\right) \right\}$
3. Soal EBTANAS Matematika IPA SMA 1989
Himpunan penyelesaian sistem persamaan
$\left\{\begin{matrix}
y=x^{2}-2x+5 \\
y=4x
\end{matrix}\right.$
adalah...
$\begin{align}
(A)\ & \left\{ \left(5,-20 \right),\ \left(1,-4 \right) \right\} \\
(B)\ & \left\{ \left(-5,-20 \right),\ \left(-1,-4 \right) \right\} \\
(C)\ & \left\{ \left(5, 20 \right),\ \left(1, 4 \right) \right\} \\
(D)\ & \left\{ \left(-5, 20 \right),\ \left(-1, 4 \right) \right\} \\
(E)\ & \left\{ \left(5, 20 \right),\ \left(-1, 4 \right) \right\} \\
\end{align}$
Show
Langkah pertama kita subsitusi nilai $y$ pada persamaan linear dan $y$ persamaan kuadrat, dapat kita tuliskan:
$\begin{align}
y &= y \\
x^{2}-2x+5 & = 4x \\
x^{2}-2x-4x+5 & = 0 \\
x^{2}-6x + 5 & = 0 \\
\left(x-5 \right)\left(x-1 \right) &= 0 \\
x=5\ \text{atau}\ x=1 & \\
\end{align}$
Langkah kedua, menentukan himpunan penyelesaian sistem persamaan:
- untuk $x=1$ maka $y=4x=4$ kita peroleh titik potong $(1,4)$
- untuk $x=5$ maka $y=4x=20$ kita peroleh titik potong $(5,20)$
- Himpunan Penyelesaian adalah $\left\{ \left(1,4 \right),\ \left(5,20 \right) \right\}$
4. Soal EBTANAS Matematika IPA SMA 1986
Jika himpunan penyelesaian sistem persamaan
$\left\{\begin{matrix}
x-y=1 \\
x^{2}-xy+y^{2}=7
\end{matrix}\right.$
adalah $\left\{ \left(x_{1},y_{1} \right),\ \left(x_{2},y_{2} \right) \right\}$ maka nilai $y_{1}+y_{2}=\cdots$
$\begin{align}
(A)\ & -2 \\
(B)\ & -1 \\
(C)\ & 0 \\
(D)\ & 1 \\
(E)\ & 2 \\
\end{align}$
Show
Langkah pertama kita subsitusi nilai $y$ pada persamaan linear dan $y$ persamaan kuadrat, dapat kita tuliskan:
$\begin{align}
x^{2}-xy+y^{2} &= 7 \\
x^{2}-x\left(x-1 \right)+\left(x-1 \right)^{2} -7 &= 0 \\
x^{2}-x^{2}+x+ x^{2}-2x+1 -7 &= 0 \\
x^{2}-x-6 &= 0 \\
\left(x-3 \right)\left(x+2 \right) &= 0 \\
x=3\ \text{atau}\ x=-2 & \\
\end{align}$
Langkah kedua, menentukan himpunan penyelesaian sistem persamaan:
- untuk $x=-2$ maka $y=x-1=-3$ kita peroleh titik potong $(-2,-3)$
- untuk $x=3$ maka $y=x-1=2$ kita peroleh titik potong $(3,2)$
- Himpunan Penyelesaian adalah $\left\{ \left(-2,-3 \right),\ \left(3,2 \right) \right\}$
$\therefore$ Pilihan yang sesuai adalah $(B)\ -1$
5. Soal SIMAK UI 2009 Kode 921
Jika suatu garis lurus yang melalui titik $(0,-14)$ tidak memotong maupun meyinggung parabola $y=2x^{2}+5x-12$ maka gradien garis tersebut adalah...
$\begin{align}
(A)\ & m \lt -9 \\
(B)\ & m \lt -1 \\
(C)\ & -1 \lt m \lt -9 \\
(D)\ & 1 \lt m \lt 9 \\
(E)\ & m \gt -9
\end{align}$
show
Kita misalkan garis lurus melalui titik $(0,-14)$ dengan gradien $m$ yaitu $y=mx-14$.
Karena garis tersebut tidak memotong maupun meyinggung parabola $y=2x^{2}+5x-12$ maka diskriminan persamaan kuadrat persekutuan kurang dari nol $(D \lt 0)$.
$\begin{align}
y & = y \\
2x^{2}+5x-12 & = mx-14 \\
2x^{2}+5x-12-mx+14 & = 0 \\
2x^{2}+(5-m)x+2 & = 0 \\
\hline
D & \lt 0 \\
b^{2}-4ac & \lt 0 \\
(5-m)^{2}-4(2)(2) & \lt 0 \\
m^{2}-10m+25-16 & \lt 0 \\
m^{2}-10m+9 & \lt 0 \\
(m-9)(m-1) & \lt 0 \\
1 \lt m \lt 9
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ 1 \lt m \lt 9$
6. Soal SNMPTN 2008 Kode 211
Garis $g$ melalui titik $(0,1)$ dan menyinggung parabola $y=4x-x^{2}$. Jika titik singgungnya terletak di kaudran pertama, maka gradien garis $g$ adalah...
$\begin{align}
(A)\ & 6 \\
(B)\ & 2 \\
(C)\ & 1 \\
(D)\ & \dfrac{1}{2} \\
(E)\ & \dfrac{1}{6}
\end{align}$
show
Misal garis $g$ adalah $y=mx+1$ karena melalui $(0,1)$.
Karena garis $y=mx+1$ menyinggung $y=4x-x^{2}$ sehingga berlaku:
$\begin{align}
mx+1 & = 4x-x^{2} \\
x^{2}-4x+mx+1 & = 0 \\
x^{2}+(m-4)x+1 & = 0 \\
\hline
D & = 0 \\
b^{2}-4ac & = 0 \\
(m-4)^{2}-4(1)(1) & = 0 \\
m^{2}-8m+16-4 & = 0 \\
m^{2}-8m+12 & = 0 \\
(m-6)(m-2) & = 0 \\
m = 6 & m = 2
\end{align}$
Garis singgung kurva $y=4x-x^{2}$ yang melalui titik $(0,1)$ adalah $y=6x+1$ dan $y=2x+1$.
Karena titik singgungnya di kuadran pertama untuk nilai $m=6$ atau $m=2$ maka gradien $m=y'=4-2x$ dihasilkan oleh $x$ positif.
$\begin{array}{c|c|cc}
m = y' & m = y' \\
6 = 4-2x & 2 = 4-2x \\
6-4 = -2x & 2-4 = -2x \\
2 = -2x & -2 = -2x \\
x = -1 & x = 1 \\
\hline
\end{array} $
$ \therefore $ Pilihan yang sesuai adalah $(E)\ 2$
7. Soal SPMB 2007 Kode 741
Agar garis $y=-10x+4$ menyinggung parabola $y=px^{2}+2x-2$ maka konstanta $p=\cdots$
$\begin{align}
(A)\ & -2 \\
(B)\ & -3 \\
(C)\ & -4 \\
(D)\ & -5 \\
(E)\ & -6
\end{align}$
show
Karena garis $y=-10x+4$ meyinggung parabola $y=px^{2}+2x-2$ maka diskrimian persamaan kuadrat persekutuan sama dengan nol ($D = 0$).
$\begin{align}
y & = y \\
px^{2}+2x-2 & = -10x+4 \\
px^{2}+2x-2+10x-4 & = 0 \\
px^{2}+12x-6 & = 0 \\
D & = 0 \\
b^{2}-4ac & = 0 \\
12^{2}-4(p)(-6) & = 0 \\
144+24p & = 0 \\
24p & =-144 \\
p & =\dfrac{-144}{24}=-6
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(E)\ -6$
8. Soal SPMB 2005 Kode 370
Jika garis $x+y=p$ menyinggung parabola $y=x^{2}-x-3$, maka konstanta $p=\cdots$
$\begin{align}
(A)\ & -3 \\
(B)\ & -2 \\
(C)\ & -1 \\
(D)\ & 0 \\
(E)\ & 1
\end{align}$
show
Garis $x+y=p$ atau $y=p-x$ menyinggung kurva $y=x^{2}-x-3$, maka berlaku diskriminan persamaan kuadrat persekutuan adalah nol $(D=0)$:
$\begin{align}
y = & y \\
x^{2}-x-3 = & p-x \\
x^{2}-x-3-p+x = & 0 \\
x^{2} -3-p = & 0 \\
D = & b^{2}-4ac \\
0 = & (0)^{2}-4(1)(-3-p) \\
0 = & 12+4p \\
4p = & -12 \\
p = & -3
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(A)\ -3$
9. Soal SPMB 2004 Kode 541
Agar garis $x+2y+k=0$ menyinggung parabola $y^{2}-2x+4=0$, maka konstanta $k=\cdots$
$\begin{align}
(A)\ & -3 \\
(B)\ & -2 \\
(C)\ & -1 \\
(D)\ & 0 \\
(E)\ & 1
\end{align}$
show
Garis $x+2y+k=0$ atau $x=-2y-k$ menyinggung kurva $y^{2}-2x+4=0$ atau $x=\dfrac{1}{2}y^{2}+2$, maka berlaku diskriminan persamaan kuadrat persekutuan adalah nol $(D=0)$:
$\begin{align}
x & = x \\
\dfrac{1}{2}y^{2}+2 & = -2y-k \\
\dfrac{1}{2}y^{2}+2+2y+k & = 0 \\
\dfrac{1}{2}y^{2} +2y+2+k & = 0
\end{align}$
$\begin{align}
D & = b^{2}-4ac \\
0 & = \left( 2 \right)^{2}-4\left( \dfrac{1}{2} \right)(2+k) \\
0 & = 4-4-2k \\
0 & = -2k \\
k & = 0
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ 0$
10. Soal SPMB 2004 Kode 241
Jika garis $y=bx-a$ memotong $y=ax^{2}+bx+(a-2b)$ di titik $(1,1)$ dan $(x_{0},y_{0})$ , maka $x_{0}+y_{0} =\cdots$
$\begin{align}
(A)\ & -6 \\
(B)\ & -5 \\
(C)\ & -4 \\
(D)\ & 0 \\
(E)\ & 2
\end{align}$
show
Garis $y=bx-a$ memotong kurva $y=ax^{2}+bx+(a-2b)$, di titik $(1,1)$ maka berlaku:
$\begin{align}
ax^{2}+bx+(a-2b) & = y \\
a(1)^{2}+b(1)+(a-2b) & = 1 \\
a +b + a-2b & = 1 \\
2a- b & = 1 \\
hline
bx-a & = y \\
b-a & = 1
\end{align}$
$\begin{array}{c|c|cc}
2a-b = 1 & \\
b-a = 1 & (+) \\
\hline
a = 2 & b=3
\end{array} $
Titik potong $y=3x-2$ memotong kurva $y=2x^{2}+3x-4$ adalah
$\begin{align}
y & = y \\
2x^{2}+3x-4 & = 3x-2 \\
2x^{2}+3x-4-3x+2 & = 0 \\
2x^{2}-2 & = 0 \\
2(x-1)(x+1) & = 0 \\
x=1\ \ x= -1
\end{align}$
Titik potong yang belum diketahui adalah untuk $x=-1$ maka $y=3x-2=3(-1)-2=-5$. Nilai $x_{0}+y_{0} =-1-5=-6$
$ \therefore $ Pilihan yang sesuai adalah $(A)\ -6$
11. Soal SPMB 2004 Kode 640
Agar kurva $y=mx^{2}-2mx+m$ seluruhnya terletak di atas kurva $y=2x^{2}-3$, maka konstanta $m$ memenuhi...
$\begin{align}
(A)\ & m \gt 6 \\
(B)\ & m \gt 2 \\
(C)\ & 2 \lt m \lt 6 \\
(D)\ & -6 \lt m \lt 2 \\
(E)\ & -6 \lt m \lt -2
\end{align}$
show
Karena kurva $y=mx^{2}-2mx+m$ seluruhnya terletak di atas kurva $y=2x^{2}-3$ artinya kedua kurva tidak pernah berpotongan atau bersinggungan maka persamaan kuadrat persekutuan merupakan definit positif maka $a \gt 0$ dan $D \lt 0$.
$\begin{align}
y & = y \\
mx^{2}-2mx+m & = 2x^{2}-3 \\
mx^{2}-2mx+m -2x^{2}+3& = 0 \\
(m-2)x^{2}-2mx+m+3& = 0 \\
\hline
a & \gt 0 \\
m-2 & \gt 0 \\
m & \gt 2 \\
\hline
D & \lt 0 \\
b^{2}-4ac & \lt 0 \\
(-2m)^{2}-4(m-2)(m+3) & \lt 0 \\
4m^{2}-4m^{2}-4m+24 & \lt 0 \\
-4m & \lt -24 \\
m & \gt \dfrac{-24}{-4} \\
m & \gt 6
\end{align}$
Irisan $m \gt 2$ dan $m \gt 6$ adalah $m \gt 6$
$ \therefore $ Pilihan yang sesuai adalah $(A)\ m \gt 6 $
12. Soal SPMB 2004 Kode 241
Jika garis $y=2x+5$ menyinggung parabola $y=ax^{2}-4x+2$, maka nilai $a$ adalah...
$\begin{align}
(A)\ & -3 \\
(B)\ & -2 \\
(C)\ & -1 \\
(D)\ & 1 \\
(E)\ & 2
\end{align}$
show
Garis $y=2x+5$ menyinggung kurva $y=ax^{2}-4x+2$, maka berlaku diskriminan persamaan kuadrat persekutuan adalah nol $(D=0)$:
$\begin{align}
y & = y \\
ax^{2}-4x+2 & =2x+5 \\
ax^{2}-4x+2-2x-5 & = 0 \\
ax^{2}-6x-3 & = 0 \\
\hline
D & = 0 \\
b^{2}-4ac & = 0 \\
(-6)^{2}-4(a)(-3) & = 0 \\
36+12a & = 0 \\
12a & = -36 \\
a & = -3
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(A)\ -3$
13. Soal SPMB 2004 Kode 241
Titik potong parabola $y=mx^{2}+ x+m$, $m \neq 0$ dengan garis $y=(m+1)x+1$ adalah $\left(x_{1},y_{1} \right)$ dan $\left(x_{2},y_{2} \right)$. Jika $x_{1}^{2}+x_{2}^{2}=1$ maka nilai $m$ adalah...
$\begin{align}
(A)\ & -2 \\
(B)\ & -1 \\
(C)\ & 0 \\
(D)\ & 1 \\
(E)\ & 2
\end{align}$
show
Garis $y=(m+1)x+1$ memotong parabola $y=mx^{2}+x+m$, di titik $\left(x_{1},y_{1} \right)$ dan $\left(x_{2},y_{2} \right)$ maka berlaku:
$\begin{align}
y_{1} & = y_{1} \\
mx_{1}^{2}+ x_{1}+m & = (m+1)x_{1}+1 \\
mx_{1}^{2}+ x_{1}+m & = mx_{1}+x_{1}+1 \\
mx_{1}^{2}+ x_{1}+m -mx_{1}-x_{1}-1 & = 0 \\
mx_{1}^{2}-mx_{1}+m-1 & = 0 \\
\hline
y_{2} & = y_{2} \\
mx_{2}^{2}-mx_{2}+m-1 & = 0 \\
\end{align}$
Karena $mx_{1}^{2}-mx_{1}+m-1= 0$ dan $mx_{2}^{2}-mx_{2}+m-1 = 0$ maka persamaan kuadrat $mx^{2}-mx+m-1= 0$ akar-akarnya adalah $x_{1}$ dan $x_{2}$. Sehingga berlaku:
$\begin{align}
x_{1}+x_{2} & = -\dfrac{b}{a} \\
& = -\dfrac{-m}{m}=1 \\
\left( x_{1}+x_{2} \right)^{2} & = 1 \\
x_{1}^{2}+x_{2}^{2}+2x_{1}x_{2} & = 1 \\
1+2x_{1}x_{2} & = 1 \\
2x_{1}x_{2} & = 1-1 \\
\dfrac{c}{a} & = 0 \\
\dfrac{m-1}{m} & = 0 \\
m-1 & = 0 \\
m & = 1
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ 1$
14. Soal UM UGM 2014 Kode 521
Jika garis $2x-3y+5k-1=0$ memotong parabola $y=x^{2}-2x+k+1$ di dua titik maka nilai $k$ yang memenuhi adalah...
$\begin{align}
(A)\ & k \lt -\dfrac{3}{2} \\
(B)\ & k \lt -\dfrac{2}{3} \\
(C)\ & k \gt -\dfrac{2}{3} \\
(D)\ & k \lt \dfrac{2}{3} \\
(E)\ & k \lt \dfrac{3}{2}
\end{align}$
show
Pada soal garis $2x-3y+5k-1=0$ atau $y=\dfrac{2}{3}x+\dfrac{5k-1}{3}$ memotong parabola $y=x^{2}-2x+k+1$ di dua titik, sehingga pernah terjadi;
$\begin{align}
y &= y \\
x^{2}-2x+k+1 &= \dfrac{2}{3}x+\dfrac{5k-1}{3} \\
3x^{2}-6x+3k+3 &= 2x+ 5k-1 \\
3x^{2}-6x+3k+3-2x -5k+1 &= 0 \\
3x^{2}-8x-2k+4 &= 0
\end{align}$
Karena garis memotong parabola di dua titik maka diskriminan $3x^{2}-8x-2k+4 = 0$ harus lebih dari nol;
$\begin{align}
D & \gt 0 \\
b^{2}-4ac & \gt 0 \\
(-8)^{2}-4(3)(-2k+4) & \gt 0 \\
64+24k-48 & \gt 0 \\
24k+16 & \gt 0 \\
k & \gt \dfrac{-16}{24} \\
k & \gt \dfrac{-2}{3}
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ k \gt -\dfrac{2}{3} $
15. Soal SBMPTN 2014 Kode 652
Jika $2a+1 \lt 0$ dan grafik $y=x^{2}-4ax+a$ bersinggungan dengan grafik $y=2x^{2}+2x$, maka $a^{2}+1=\cdots$
$\begin{align}
(A)\ & \dfrac{17}{16} \\
(B)\ & \dfrac{5}{4} \\
(C)\ & 2 \\
(D)\ & 5 \\
(E)\ & 17
\end{align}$
show
Grafik $y=x^{2}-4ax+a$ bersinggungan dengan grafik $y=2x^{2}+2x$ maka diskriminan persekutuan adalah nol;
$\begin{align}
y &= y \\
2x^{2}+2x &= x^{2}-4ax+a \\
2x^{2}+2x - x^{2}+4ax-a &= 0 \\
x^{2}+2x+4ax-a &= 0 \\
x^{2}+(2+4a)x-a &= 0
\end{align}$
$\begin{align}
D & = 0 \\
b^{2}-4ac & = 0 \\
(2+4a)^{2}-4(1)(-a) & = 0 \\
16a^{2}+16a+4+4a & = 0 \\
16a^{2}+20a+4 & = 0 \\
4a^{2}+5a+1 & = 0 \\
(4a+1)( a+1) & = 0 \\
a & = -\dfrac{1}{4} \\
a & = -1
\end{align}$
Nilai $a$ yang memenuhi $2a+1 \lt 0$ adalah $a=-1$ sehingga nilai $a^{2}+1=(-1)^{2}+1=2$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ 2 $
16. Soal UM STIS 2011
Jumlah $x$ dan $y$ dari solusi $(x,y)$ yang memenuhi sistem persamaan
$\begin{array}{cc}
x-y = a & \\
x^{2}+5x-y = 2 & \\
\end{array} $
adalah...
$\begin{align}
(A)\ & -12 \\
(B)\ & -10 \\
(C)\ & -6 \\
(D)\ & 6 \\
(E)\ & 10
\end{align}$
show
Catatan calon guru tentang sistem persamaan mungkin dapat membantu yaitu Karena garis $y=mx+n$ dan parabola $y=ax^{2}+bx+c$ mempunyai satu solusi saat diskrimian persamaan kuadrat persekutuan sama dengan nol $(D=b^{2}-4ac = 0)$.
$\begin{align}
x^{2}+5x-y &= 2 \\
x^{2}+5x-(x-a) &= 2 \\
x^{2}+5x- x+a-2 &= 0 \\
x^{2}+4x+a-2 &= 0 \\
\hline
D &= b^{2}-4ac \\
0 &= 4^{2}-4(1)(a-2) \\
0 &= 16-4a+8 \\
4a &= 24 \\
a &= 6 \\
\hline
x^{2}+4x+6-2 &= 0 \\
x^{2}+4x+4 &= 0 \\
(x+2)(x+2) &= 0 \\
x=-2 & \\
x-y &= a \\
-2-y &= 6 \\
y &= -8 \\
x+y &= -10
\end{align}$
$\therefore$ Pilihan yang sesuai $(B)\ -10$
17. Soal UM STIS 2011
Jika persamaan garis singgung kurva $y=ax^{2}-bx+3$ pada titik $(1,1)$ tegak lurus garis $6y-x+7=0$, maka $a^{2}+b^{2}=\cdots$
$\begin{align}
(A)\ & 8 \\
(B)\ & 10 \\
(C)\ & 13 \\
(D)\ & 20 \\
(E)\ & 52
\end{align}$
show
Catatan calon guru yang mungkin kita perlukan tentang persamaan garis yaitu:
- $m_{1} \cdot m_{2}=-1$ saat $g_{1}$ tegak lurus dengan $g_{2}$ atau saat $g_{1} \perp g_{2}$ maka $m_{1} \cdot m_{2}=-1$;
- Untuk sebuah fungsi $f(x)$ gradien di titik $(a,b)$ adalah turunan pertama fungsi untuk $x=a$ yaitu $m=f'(a)$
Pada titik $(1,1)$ dan $y=ax^{2}-bx+3$ maka $1=a(1)^{2}-b(1)+3$ atau $ a -b=-2$
Gradien garis $6y-x+7=0$ adalah $m=-\dfrac{-1}{6}=\dfrac{1}{6}$
Gradien garis singgung kurva $y=ax^{2}-bx+3$ di $(1,-1)$ adalah $m=-6$, maka berlaku
$\begin{align}
y & = ax^{2}-bx+3 \\
m=y' & = 2ax -b \\
-6 & = 2a(1) -b \\
-6 & = 2a -b
\end{align}$
$\begin{array}{c|c|cc}
2a-b = -6 & \\
a-b = -2 & (-) \\
\hline
a = -4 & \\
b = -2 & \\
\hline
a^{2}+b^{2} = (-4)^{2}+(-2)^{2} & \\
a^{2}+b^{2} = 20
\end{array} $
$\therefore$ Pilihan yang sesuai $(D)\ 20$
18. Soal UTBK-SBMPTN 2019
Diketahui sistem persamaan
$\left\{\begin{matrix}
y=-mx+c\\
y= \left ( x+4 \right )^{2}
\end{matrix}\right.$
Jika sistem persamaan tersebut memiliki tepat satu penyelesaian, maka jumlah semua nilai $m$ adalah...
$\begin{align}
(A)\ & -32 \\
(B)\ & -20 \\
(C)\ & -16 \\
(D)\ & -8 \\
(E)\ & -4
\end{align}$
show
Karena sistem persamaan di atas memiliki tepat satu penyelesaian maka diskriminan $(D=b^{2}-4ac)$ dari persekutuan persamaan kuadrat adalah nol.
$\begin{align}
y & = y \\
\left ( x+4 \right )^{2} & = -mx+c \\
x^{2}+8x+16 +mx -c & = 0 \\
x^{2}+(8+m)x+16-c & = 0 \\
b^{2}-4ac & = 0 \\
(8+m)^{2} -4(1)(16-c) & = 0 \\
m^{2}+16m+64-64+4c & = 0 \\
m^{2}+16m+4c & = 0 \\
m_{1} + m_{2} & = -\dfrac{b}{a}\\
&=-\dfrac{16}{1}=-16
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ -16$
19. Soal UTBK-SBMPTN 2019
Jika $(a,b)$ solusi dari sistem persamaan kuadrat
$\left\{\begin{matrix}
x^{2}+y^{2}-2x=19\\
x+y^{2}=1
\end{matrix}\right.$
maka nilai $a+4b$ yang terbesar adalah...
$\begin{align}
(A)\ & 4 \\
(B)\ & 5 \\
(C)\ & 10 \\
(D)\ & 11 \\
(E)\ & 14
\end{align}$
show
Dari sistem persamaan dapat kita peroleh nilai $a$ dan $b$, yaitu:
$\begin{align}
x^{2}+y^{2}-2x &=19 \\
x^{2}+(1-x)-2x &=19 \\
x^{2}-3x+-18 &= 0 \\
(x-6)(x+3) & = 0 \\
x=6\ \text{atau}\ x=-3 & \\
\hline
y^{2}=1-x & \\
\hline
x=6\ \Rightarrow\ & y^{2}=-5\ (imajiner) \\
x=-3\ \Rightarrow\ & y^{2}=4 \\
& y=2\ \text{atau}\ y=-2 \\
\hline
(-3,2)\ \Rightarrow\ & a+4b=5 \\
(-3,-2)\ \Rightarrow\ & a+4b=-11
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(B)\ 5$
20. Soal UTBK-SBMPTN 2019
Himpunan $(x,y)$ adalah penyelesaian dari sistem persamaan
$\left\{\begin{matrix}
x^{2}+y^{2}=6\\
\dfrac{x^{2}}{2}+\dfrac{y^{2}}{8}=3
\end{matrix}\right.$
Jumlah dari semua nilai $x$ yang memenuhi adalah...
$\begin{align}
(A)\ & -2 \\
(B)\ & -1 \\
(C)\ & 0 \\
(D)\ & 1 \\
(E)\ & 2
\end{align}$
show
Dari sistem persamaan dapat kita peroleh nilai $a$ dan $b$, yaitu:
$\begin{align}
\dfrac{x^{2}}{2}+\dfrac{y^{2}}{8} &=3 \\
8x^{2} + 2y^{2} &=48 \\
8x^{2} + 2 \left( 6-x^{2} \right) &=48 \\
8x^{2} + 12-2x^{2}-48&=0 \\
6x^{2}- 36 &=0 \\
x^{2}- 6 &=0 \\
(x-\sqrt{6})(x+\sqrt{6}) &=0 \\
x=\sqrt{6}\ \text{atau}\ x=-\sqrt{6} & \\
\hline
y^{2}=6-x^{2} & \\
\hline
x=\sqrt{6}\ \Rightarrow\ & y^{2}=0 \\
x=-\sqrt{6}\ \Rightarrow\ & y^{2}=0 \\
\end{align}$
Jumlah semua nilai $x$ dan $y$ yang memenuhi adalah $0$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ 0$
21. Soal UTBK-SBMPTN 2019
Diketahui sistem persamaan
$\left\{\begin{matrix}
x^{2}+y^{2}+2y=8\\
x^{2}-y^{2}-2y+4x+8=0
\end{matrix}\right.$
Mempunyai solusi $(x,y)$ dengan $x$ dan $y$ bilangan real. Jumlah semua ordinatnya adalah...
$\begin{align}
(A)\ & 4 \\
(B)\ & 2 \\
(C)\ & 0 \\
(D)\ & -2 \\
(E)\ & -4
\end{align}$
show
Dari sistem persamaan dapat kita peroleh nilai $a$ dan $b$, yaitu:
$\begin{align}
x^{2}+y^{2}+2y-8 &= 0 \\
x^{2}-y^{2}-2y+4x+8 & = 0 \ \ (+) \\
\hline
2x^{2}+4x &=0 \\
x^{2}+2x &=0 \\
x(x+2) &=0 \\
x=0\ \text{atau}\ x=-2 & \\
\hline
x=0\ & \Rightarrow\ -y^{2}-2y+8=0 \\
& \Rightarrow\ y^{2}+2y-8=0 \\
& \Rightarrow\ y_{1}+y_{2} =-2 \\
\hline
x=-2\ & \Rightarrow\ -y^{2}-2y+8=4 \\
& \Rightarrow\ y^{2}+2y-4=0 \\
& \Rightarrow\ y_{1}+y_{2} =-2
\end{align}$
Jumlah semua ordinatnya adalah $(-2)+(-2)=-4$
$ \therefore $ Pilihan yang sesuai adalah $(E)\ -4$
22. Soal UTBK-SBMPTN 2019
Diketahui
$\left\{\begin{matrix}
x^{2}+y^{2}-2y=13\\
x^{2}-y=1
\end{matrix}\right.$
maka nilai $x^{2}+2y$ adalah...
$\begin{align}
(A)\ & 10 \\
(B)\ & 11 \\
(C)\ & 12 \\
(D)\ & 13 \\
(E)\ & 14
\end{align}$
show
Dari sistem persamaan dapat kita peroleh nilai $a$ dan $b$, yaitu:
$\begin{align}
x^{2}+y^{2}-2y &=13 \\
y+1+y^{2}-2y &=13 \\
y^{2}-y -12&= 0 \\
(y-4)(y+3) & = 0 \\
y=4\ \text{atau}\ y=-3 & \\
\hline
x^{2}=y+1 & \\
\hline
y=4\ & \Rightarrow\ x^{2}=5 \\
& \rightarrow\ x^{2}+2y=13 \\
y=-3\ & \Rightarrow\ x^{2}=-2\ (imajiner) \\
& \rightarrow\ x^{2}+2y=-8
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ 13$
23. Soal UTBK-SBMPTN 2019
Jika $(a,b)$ solusi dari sistem persamaan
$\left\{\begin{matrix}
x^{2}+y^{2}=5 \\
x-y^{2}=1
\end{matrix}\right.$
maka nilai $a-3b$ yang terkecil adalah...
$\begin{align}
(A)\ & 5 \\
(B)\ & 1 \\
(C)\ & 0 \\
(D)\ & -1 \\
(E)\ & -5
\end{align}$
show
Dari sistem persamaan dapat kita peroleh nilai $a$ dan $b$, yaitu:
$\begin{align}
x^{2}+y^{2} &= 5 \\
x^{2}+(x-1) &= 5 \\
x^{2}+x-6 &= 0 \\
(x+3)(x-2) & = 0 \\
x=-3\ \text{atau}\ x=2 & \\
\hline
y^{2}=x-1 & \\
\hline
x=-3\ \Rightarrow\ & y^{2}=-4\ (imajiner) \\
x=2\ \Rightarrow\ & y^{2}=1 \\
& y=1\ \text{atau}\ y=-1 \\
\hline
(2,1)\ \Rightarrow\ & a-3b=-1 \\
(2,-1)\ \Rightarrow\ & a-3b=5
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ -1$
24. Soal UTBK-SBMPTN 2019
Diketahui sistem persamaan
$\left\{\begin{matrix}
x^{2}+y=16\\
x^{2}+y^{2}-11y=-19
\end{matrix}\right.$
Mempunyai solusi $(x,y)$ dengan $x$ dan $y$ bilangan real. Jumlah semua ordinatnya adalah...
$\begin{align}
(A)\ & 12 \\
(B)\ & 10 \\
(C)\ & 35 \\
(D)\ & -10 \\
(E)\ & -12
\end{align}$
show
Dari sistem persamaan dapat kita peroleh:
$\begin{align}
x^{2}+y^{2}-11y &=-19 \\
16-y+y^{2}-11y &=-19 \\
y^{2}-12y+35 &=0 \\
\hline
y_{1}+y_{2} &= -\dfrac{b}{a} \\
&= -\dfrac{-12}{1}=12
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(A)\ 12$
25. Soal UTBK-SBMPTN 2019
Jika garis $y=2x-3$ menyinggung parabola $y=4x^{2}+ax+b$ di titik $(-1,-5)$ serta $a$ dan $b$ adalah konstanta, maka $a+b=\cdots$
$\begin{align}
(A)\ & 8 \\
(B)\ & 9 \\
(C)\ & 10 \\
(D)\ & 11 \\
(E)\ & 12
\end{align}$
show
Titik $(-1,-5)$ adalah titik singgung sehingga berlaku:
$ \begin{align}
y & =4x^{2}+ax+b \\
-5 & =4(-1)^{2}+a(-1)+b \\
-5 & =4 -a+b \\
-9 & = -a+b \\
a-9 & = b
\end{align} $
Sedikit catatan calon guru yang mungkin kita butuhkan yaitu jika garis $y=2x-3$ menyinggung parabola $y=4x^{2}+ax+b$ maka berlaku diskriminan persamaan kuadrat persekutuan adalah nol $(D=0)$:
$\begin{align}
y & = y \\
4x^{2}+ax+b & = 2x-3 \\
4x^{2}+ax-2x+b+3 & = 0 \\
4x^{2}+(a -2)x+b+3 & = 0 \\
\hline
D & = 0 \\
b^{2}-4ac & = 0 \\
(a-2)^{2}-4(4)(b+3) & = 0 \\
a^{2}-4a+4-16b-48 & = 0 \\
a^{2}-4a -16(a-9)-44 & = 0 \\
a^{2}-4a -16 a+144-44 & = 0 \\
a^{2}-20a+100 & = 0 \\
(a-10) (a-10) &=0 \\
a=10 & \\
\hline
a+b & =10+1=11
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(D)\ 11$
26. Soal UTBK-SBMPTN 2019
Jika garis $y=mx$ menyinggung elips $\dfrac{(x-2)^{2}}{4}+\dfrac{(y+1)^{2}}{2}=1$, maka nilai $4m=\cdots$
$\begin{align}
(A)\ & 1 \\
(B)\ & 2 \\
(C)\ & 0 \\
(D)\ & -2 \\
(E)\ & -1
\end{align}$
show
Sedikit catatan calon guru yang mungkin kita butuhkan pada sistem persamaan yaitu jika garis $y=mx$ menyinggung elips $\dfrac{(x-2)^{2}}{4}+\dfrac{(y+1)^{2}}{2}=1$ maka berlaku diskriminan persamaan kuadrat persekutuan adalah nol $(D=0)$:
$\begin{align}
\dfrac{(x-2)^{2}}{4}+\dfrac{(y+1)^{2}}{2} &=1 \\
(x-2)^{2} + 2(mx+1)^{2} &=4 \\
x^{2}-4x+4 + 2m^{2}x^{2}+4mx+2 &=4 \\
\left(2m^{2}+1\right)x^{2}+(4m-4)x+2 &=0 \\
\hline
D & = 0 \\
b^{2}-4ac & = 0 \\
(4m-4)^{2}-4\left(2m^{2}+1\right)(2) & = 0 \\
16m^{2}-32m-16m^{2}-8 & = 0 \\
-32m -8 & = 0 \\
-32m & = 8 \\
m & = -\dfrac{8}{32}=-\dfrac{1}{4} \\
4m &= 1
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(A)\ 1$
27. Soal UTBK-SBMPTN 2019
Garis $y=2x+1$ tidak memotong maupun menyinggung hiperbola $\dfrac{(x-2)^{2}}{2}-\dfrac{(y-a)^{2}}{4}=1$, interval nilai $a$ yang memenuhi adalah....
$\begin{align}
(A)\ & -7 \lt a \lt 3 \\
(B)\ & -3 \lt a \lt 7 \\
(C)\ & a \lt 3\ \text{atau}\ a \gt 7 \\
(D)\ & a \lt -7\ \text{atau}\ a \gt 3 \\
(E)\ & 3 \lt a \lt 7
\end{align}$
show
Sedikit catatan calon guru yang mungkin kita butuhkan pada sistem persamaan yaitu jika garis $y=2x+1$ tidak memotong maupun menyinggung hiperbola $\dfrac{(x-2)^{2}}{2}-\dfrac{(y-a)^{2}}{a}=1$ maka berlaku diskriminan persamaan kuadrat persekutuan kurang dari nol $(D \lt 0)$:
$\begin{align}
\dfrac{(x-2)^{2}}{2}-\dfrac{(y-a)^{2}}{4} &=1 \\
\dfrac{x^{2}-4x+4}{2}-\dfrac{y^{2}-2ay+a^{2}}{4} &=1 \\
2x^{2}-8x+8 - y^{2}+2ay-a^{2} &=4 \\
2x^{2}-8x+8 - (2x+1)^{2}+2a(2x+1)-a^{2} &=4 \\
2x^{2}-8x+8 - \left( 4x^{2}+4x+1 \right)+4ax +2a-a^{2} &=4 \\
-2x^{2}-12x+4ax-a^{2}+2a+3 &= 0 \\
2x^{2}+(12 -4a)x+a^{2}-2a-3 &= 0 \\
\hline
D & \lt 0 \\
b^{2}-4ac & \lt 0 \\
(12-4a)^{2}-4 (2) \left( a^{2}-2a-3 \right) & \lt 0 \\
144-96a+16a^{2}-8a^{2}+16a+24 & \lt 0 \\
8a^{2}-80a +168 & \lt 0 \\
a^{2}- 10a +21 & \lt 0 \\
(a-3)(a-7) & \lt 0
\end{align}$
Himpunan penyelesaian pertidaksamaan kuadrat di atas adalah $3 \lt a \lt 7 $
$\therefore$ Pilihan yang sesuai adalah $(E)\ 3 \lt a \lt 7 $
28. Soal UTBK-SBMPTN 2019
Diketahui grafik $y=8x+a$ dan $y=x^{2}+5x$ berpotongan di dua titik $\left(x_{1},y_{1} \right)$ dan $\left(x_{2},y_{2} \right)$. Jika grafik $y=x^{2}+5x$ melalui titik $(a,-6)$, maka $x_{1}x_{2}=\cdots$
$\begin{align}
(A)\ & -3 \\
(B)\ & -2 \\
(C)\ & -1 \\
(D)\ & 1 \\
(E)\ & 2
\end{align}$
show
Disampaikan pada soal bahwa grafik $y=x^{2}+5x$ melalui titik $(a,-6)$ sehingga berlaku:
$\begin{align}
y &= x^{2}+5x \\
-6 &= a^{2}+5a \\
0 &= a^{2}+5a +6 \\
(a+2)(a+3) &= 0 \\
a=-2\ \text{atau}\ & a=-3
\end{align}$
Untuk $a=-2$ pada grafik $y=8x+a$ dan $y=x^{2}+5x$ berlaku:
$\begin{align}
8x+a &= x^{2}+5x \\
8x-2 &= x^{2}+5x \\
x^{2}+5x-8x+2 &= 0 \\
x^{2}-3x+2 &= 0 \\
\hline
x_{1}x_{2} &= \dfrac{c}{a} \\
&= \dfrac{2}{1}=2
\end{align}$
$\therefore$ Pilihan yang sesuai adalah $(E)\ 2$
29. Soal UTBK-SBMPTN 2019
Diketahui grafik $y=-x^{2}+4ax-6a$ memotong sumbu-$x$ di titik $(2,0)$ dan $(6,0)$. Jika garis $mx-y=12$ memotong grafik tersebut di titik $(6,0)$ dan $\left(x_{0},y_{0} \right)$, maka $ x_{0}-y_{0}=\cdots$
$\begin{align}
(A)\ & 10 \\
(B)\ & 12 \\
(C)\ & 14 \\
(D)\ & 16 \\
(E)\ & 18
\end{align}$
show
Disampaikan pada soal bahwa grafik $y=-x^{2}+4ax-6a$ memotong sumbu-$x$ di titik $(2,0)$ dan $(6,0)$ sehingga berlaku:
$\begin{align}
y &=-x^{2}+4ax-6a \\
(2,0) \rightarrow 0 &=-(2)^{2}+4a(2)-6a \\
0 &= -4+8a-6a \\
4 &= 8a-6a \\
4 &= 2a \\
2 &= a
\end{align}$
Untuk $a= 2$ maka grafik $y=-x^{2}+4ax-6a$ adalah $y=-x^{2}+8x-12$.
Garis $mx-y=12$ memotong grafik $y=-x^{2}+8x-12$ di titik $(6,0)$ sehingga dapat berlaku:
$\begin{align}
(6,0) \rightarrow y &=mx-12 \\
0 &=m(6)-12 \\
m &=2 \\
y &=2x-12
\end{align}$
Garis $y=2x-12$ memotong grafik $y=-x^{2}+8x-12$ di titik $(6,0)$ dan $\left(x_{0},y_{0} \right)$ sehingga dapat berlaku:
$\begin{align}
y &= y \\
2x-12 &= -x^{2}+8x-12 \\
0 &= -x^{2}+8x-2x-12+12 \\
0 &= -x^{2}+6x \\
x^{2}-6x &= 0 \\
(x)(x-6) &= 0 \\
x=0\ \text{atau}\ & x=6 \\
\hline
x=0 \rightarrow & y=2x-12 \\
& y=2(0)-12=-12 \\
\end{align}$
Nilai $x_{0}-y_{0}=0-(-12)=12$.
$\therefore$ Pilihan yang sesuai adalah $(B)\ 12$
30. Soal UTBK-SBMPTN 2019
Agar sistem pertidaksamaan kuadrat di bawah ini hanya mempunyai satu solusi
$\left\{\begin{matrix}
y=-mx^{2}-2 \\
4x^{2}+y^{2}=4
\end{matrix}\right.$
Nilai $m$ adalah...
$\begin{align}
(A)\ & \dfrac{1}{3} \\
(B)\ & \dfrac{1}{\sqrt{2}} \\
(C)\ & 1 \\
(D)\ & \sqrt{2} \\
(E)\ & \sqrt{3} \\
\end{align}$
show
Karena sistem persamaan di atas memiliki tepat satu penyelesaian maka diskriminan $(D=b^{2}-4ac)$ dari persamaan kuadrat persekutuan adalah nol.
Persamaan $y=-mx^{2}-2$ kita ubah menjadi $\dfrac{y+2}{-m}=x^{2}$ lalu kita substitusikan ke $4x^{2}+y^{2}=4$ dan kita peroleh persamaan kuadrat baru.
$\begin{align}
4x^{2}+y^{2} &= 4 \\
4 \left( \dfrac{y+2}{-m} \right)+y^{2} &= 4 \\
-4y+8+my^{2} &= 4m \\
my^{2}-4y+8-4m &= 0 \\
\hline
b^{2}-4ac & = 0 \\
(-4)^{2} -4(m)(8-4m) & = 0 \\
16-32m+16m^{2} & = 0 \\
16m^{2}-32m+16 & = 0 \\
m^{2}-2m+1 & = 0 \\
(m-1)^{2} & = 0 \\
m & = 1
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(C)\ 1$
31. Soal UTBK-SBMPTN 2019
Agar sistem pertidaksamaan kuadrat di bawah ini hanya mempunyai satu solusi
$\left\{\begin{matrix}
x^{2}+y^{2} = 4 \\
(x-1)^{2}+my^{2}=1
\end{matrix}\right.$
Nilai $m$ adalah...
$\begin{align}
(A)\ & \dfrac{1}{4} \\
(B)\ & \dfrac{1}{2} \\
(C)\ & 1 \\
(D)\ & -\dfrac{1}{2} \\
(E)\ & - \dfrac{1}{4} \\
\end{align}$
show
Karena sistem persamaan di atas memiliki tepat satu penyelesaian maka diskriminan $(D=b^{2}-4ac)$ dari persamaan kuadrat persekutuan adalah nol.
Persamaan $x^{2}+y^{2} = 4$ kita ubah menjadi $y^{2}= 4-x^{2}$ lalu kita substitusikan ke $(x-1)^{2}+my^{2}=1$ dan kita peroleh persamaan kuadrat baru.
$\begin{align}
(x-1)^{2}+my^{2} &=1 \\
(x-1)^{2}+m \left( 4-x^{2} \right) &=1 \\
x^{2}-2x+1+4m-mx^{2} &=1 \\
(m-1)x^{2}+2x-4m &= 0 \\
\hline
b^{2}-4ac & = 0 \\
(2)^{2} -4(m-1)(-4m) & = 0 \\
4 + 16m^{2}-16m & = 0 \\
\left(4m-2 \left)^{2} & = 0 \\
m=\dfrac{1}{2} &
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(B)\ \dfrac{1}{2}$
32. Soal UTBK-SBMPTN 2019
Agar sistem pertidaksamaan kuadrat di bawah ini hanya mempunyai satu solusi
$\left\{\begin{matrix}
x^{2}+y^{2} = 4 \\
(x-1)^{2}+my^{2}=1
\end{matrix}\right.$
Nilai $m$ adalah...
$\begin{align}
(A)\ & \dfrac{1}{4} \\
(B)\ & \dfrac{1}{2} \\
(C)\ & 1 \\
(D)\ & -\dfrac{1}{2} \\
(E)\ & - \dfrac{1}{4} \\
\end{align}$
show
Karena sistem persamaan di atas memiliki tepat satu penyelesaian maka diskriminan $(D=b^{2}-4ac)$ dari persamaan kuadrat persekutuan adalah nol.
Persamaan $x^{2}+y^{2} = 4$ kita ubah menjadi $y^{2}= 4-x^{2}$ lalu kita substitusikan ke $(x-1)^{2}+my^{2}=1$ dan kita peroleh persamaan kuadrat baru.
$\begin{align}
(x-1)^{2}+my^{2} &=1 \\
(x-1)^{2}+m \left( 4-x^{2} \right) &=1 \\
x^{2}-2x+1+4m-mx^{2} &=1 \\
(m-1)x^{2}+2x-4m &= 0 \\
\hline
b^{2}-4ac & = 0 \\
(2)^{2} -4(m-1)(-4m) & = 0 \\
4 + 16m^{2}-16m & = 0 \\
\left(4m-2 \right)^{2} & = 0 \\
m=\dfrac{1}{2} &
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(B)\ \dfrac{1}{2}$
33. Soal Latihan UTBK-SBMPTN 2021
Diketahui garis $g$ melalui titik $(0,-1)$ dan menyingung kurva $y^{2}+2y-2x+2=0$. Garis $g$ memotong sumbu-$x$ di titik $(a,0)$ dengan $a=\cdots$
$\begin{align}
(A)\ & -2\ \text{atau}\ 3 \\
(B)\ & -3\ \text{atau}\ 3 \\
(C)\ & -2\ \text{atau}\ 2 \\
(D)\ & -1\ \text{atau}\ 1 \\
(E)\ & 0 \\
\end{align}$
show
Untuk menyelesaikan sistem persamaan di atas kita coba dengan memisalkan garis $g$ adalah $y=mx+n$, karena garis $g$ melalui titik $(0,-1)$ sehingga garis $g$ dapat kita tuliskan menjadi $y=mx-1$.
Garis $g:\ y=mx-1$ menyingung kurva $y^{2}+2y-2x+2=0$ sehingga diskriminan persamaan kuadrat persekutuan adalah nol, atau dapat kita tuliskan penjabarannya seperti berikut:
$\begin{align}
y^{2}+2y-2x+2 &= 0 \\
\left( mx-1 \right)^{2}+2\left( mx-1 \right)-2x+2 &= 0 \\
m^{2}x^{2}-2mx+1+2mx-2-2x+2 &= 0 \\
m^{2}x^{2}-2x+1 &= 0 \\
\hline
b^{2}-4ac & = 0 \\
(-2)^{2} -4(m^{2})(1) & = 0 \\
4 -4m^{2} & = 0 \\
4m^{2} & = 4 \\
m^{2} & = 1 \\
m & = \pm 1
\end{align}$
Unttuk nilai $m=\pm 1$ sehingga garis $g:\ y=mx-n$ adalah $y=x-1$ dan $y=-x-1$ yang memotong sumbu-$x$ di titik $(-1,0)$ dan $(1,0)$.
$ \therefore $ Pilihan yang sesuai adalah $(D)\ -1\ \text{atau}\ 1$
34. Soal Latihan UTBK-SBMPTN 2021
Jika garis $y=mx+4$ tidak memotong elips $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{8}=1$, maka nilai $m$ adalah...
$\begin{align}
(A)\ & -\dfrac{1}{2} \lt m \lt \dfrac{1}{2} \\
(B)\ & -\dfrac{1}{\sqrt{2}} \lt m \lt \dfrac{1}{\sqrt{2}} \\
(C)\ & -1 \lt m \lt 1 \\
(D)\ & -\sqrt{2} \lt m \lt \sqrt{2} \\
(E)\ & -2 \lt m \lt 2
\end{align}$
show
Garis tersebut tidak memotong elips maka diskriminan persamaan kuadrat persekutuan kurang dari nol $(D \lt 0)$.
$\begin{align}
\dfrac{x^{2}}{4}+\dfrac{y^{2}}{8} &= 1 \\
2 x^{2} + y^{2} &= 8 \\
2 x^{2} + \left( mx+4 \right)^{2} &= 8 \\
2 x^{2} + m^{2}x^{2}+8mx+16-8 &= 0 \\
\left( m^{2}+2 \right)x^{2} +8mx+8 &= 0 \\
\hline
D & \lt 0 \\
\left( 8m \right)^{2}-4\left( m^{2}+2 \right)\left( 8 \right) & \lt 0 \\
64m^{2}-32m^{2}-64 & \lt 0 \\
32m^{2} -64 & \lt 0 \\
m^{2} - 2 & \lt 0 \\
(m-\sqrt{2})(m+\sqrt{2}) & \lt 0 \\
-\sqrt{2} \lt m \lt \sqrt{2}
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ -\sqrt{2} \lt m \lt \sqrt{2}$
35. Soal Latihan UTBK-SBMPTN 2021
Jika garis $y=mx$ tidak berpotongan dengan hiperbola $3x^{2}-4y^{2}=12$, maka nilai $m$ adalah...
$\begin{align}
(A)\ & \left | m \right | \gt \sqrt{\dfrac{2}{3}} \\
(B)\ & \left | m \right | \gt \dfrac{1}{2\sqrt{3}} \\
(C)\ & \left | m \right | \lt \sqrt{\dfrac{2}{3}} \\
(D)\ & \left | m \right | \gt \dfrac{\sqrt{3}}{2} \\
(E)\ & \left | m \right | \lt \dfrac{\sqrt{3}}{2}
\end{align}$
show
Garis tersebut tidak memotong hiperbola maka diskriminan persamaan kuadrat persekutuan kurang dari nol $(D \lt 0)$.
$\begin{align}
3x^{2}-4y^{2} &= 12 \\
3x^{2}-4(mx)^{2} &= 12 \\
3x^{2}-4 m^{2}x^{2} &= 12 \\
\left(3 -4 m^{2} \right)x^{2} -12 &= 0 \\
\hline
D & \lt 0 \\
\left( 0 \right)^{2}-4\left( 3 -4 m^{2} \right)\left( -12 \right) & \lt 0 \\
0-4\left( 3 -4 m^{2} \right)\left( -12 \right) & \lt 0 \\
144-192m^{2} & \lt 0 \\
192m^{2}-144 & \gt 0 \\
4m^{2}-3 & \gt 0 \\
(2m-\sqrt{3})(2m+\sqrt{3}) & \gt 0 \\
m \lt -\dfrac{\sqrt{3}}{2}\ \text{atau}\ m \gt \dfrac{\sqrt{3}}{2} & \\
\left | m \right | \gt \dfrac{\sqrt{3}}{2} & \\
\end{align}$
Simak kembali jika masih kurang paham menentukan Himpunan Penyelesaian pertidaksamaan kuadrat dengan mudah dan cepat
$ \therefore $ Pilihan yang sesuai adalah $(D)\ \left | m \right | \gt \dfrac{\sqrt{3}}{2}$
36. Soal Latihan UTBK-SBMPTN 2021
Nilai $m$ agar garis $y=mx+1$ tidak memotong hiperbola $\dfrac{x^{2}}{2} - \dfrac{y^{2}}{4} =1$ adalah...
$\begin{align}
(A)\ & m \lt -\dfrac{1}{2}\sqrt{10}\ \text{atau}\ m \gt \dfrac{1}{2}\sqrt{10} \\
(B)\ & m \lt -\dfrac{1}{2}\sqrt{5}\ \text{atau}\ m \gt \dfrac{1}{2}\sqrt{5} \\
(C)\ & m \lt -\dfrac{1}{2}\sqrt{10}\ \text{atau}\ m \gt \dfrac{1}{2}\sqrt{5} \\
(D)\ & -\dfrac{1}{2}\sqrt{10} \lt m \lt \dfrac{1}{2}\sqrt{10} \\
(E)\ & -\dfrac{1}{2}\sqrt{5} \lt m \lt \dfrac{1}{2}\sqrt{5}
\end{align}$
show
Garis tersebut tidak memotong hiperbola maka diskriminan persamaan kuadrat persekutuan kurang dari nol $(D \lt 0)$.
$\begin{align}
\dfrac{x^{2}}{2} - \dfrac{y^{2}}{4} & = 1 \\
2x^{2} - y^{2} & = 4 \\
2x^{2} - (mx+1)^{2} & = 4 \\
2x^{2} - (mx+1)^{2} - 4 & = 0 \\
2x^{2} - m^{2}x^{2}-2mx-1 - 4 & = 0 \\
\left( 2 - m^{2} \right)x^{2}-2mx - 5 & = 0 \\
\hline
D & \lt 0 \\
\left( -2m \right)^{2} - 4 \left( 2 - m^{2} \right)\left( -5 \right) & \lt 0 \\
4m^{2} + 40 - 20m^{2} & \lt 0 \\
-16m^{2} + 40 & \lt 0 \\
2m^{2} - 5 & \gt 0 \\
\left( m+\dfrac{1}{2}\sqrt{5} \right) \left( m-\dfrac{1}{2}\sqrt{5} \right) & \gt 0 \\
m \lt - \dfrac{1}{2}\sqrt{5}\ \text{atau}\ m \gt \dfrac{1}{2}\sqrt{5} &
\end{align}$
$ \therefore $ Pilihan yang sesuai adalah $(D)\ \left | m \right | \gt \dfrac{\sqrt{3}}{2}$
37. Soal UM UGM 2019 Kode 923/924
Diketahui $x^{2}+2xy+4x = -3$ dan $9y^{2}+4xy+12y = -1$. Nilai dari $x+3y$ adalah...$\begin{align} (A)\ & 2 \\ (B)\ & 1 \\ (C)\ & 0 \\ (D)\ & -1 \\ (E)\ & -2 \end{align}$
Show
$\begin{align} x^{2}+2xy+4x & = -3 \\ 9y^{2}+4xy+12y & = -1\ (+) \\ \hline x^{2}+9y^{2}+6xy+4x+12y & = -4 \\ \left(x+3y \right)^{2}+ 4\left(x+3y \right) & = -4 \\ \hline \text{misal:}\ x+3y=p & \\ \hline p^{2}+ 4p & = -4 \\ p^{2}+ 4p + 4 & = 0 \\ \left( p+2 \right)\left( p+2 \right) & =0 \\ p+2=0 & \\ p & = -2 \\ x+3y &=-2 \end{align}$
$\therefore$ Pilihan yang sesuai adalah $(E)\ -2$
38. Soal UM UGM 2019 Kode 934 |
Pada sistem persamaan berikut
\begin{array} \text{x^{2}}+xy+xz=1 \\ y^{2} +yz+yx=6 \\ z^{2}+zx+zy=9 \end{array} Nilai $z$ adalah...$\begin{align} (A)\ & \dfrac{2}{3} \\ (B)\ & 1 \\ (C)\ & \dfrac{3}{2} \\ (D)\ & \dfrac{9}{4} \\ (E)\ & 3 \end{align}$
show
Dari persamaan dapat kita peroleh:
$\begin{align} x^{2} +xy+xz &= 1 \\ y^{2} +yz+yx &= 6 \\ z^{2}+zx+zy &= 9\ (+) \\ \hline x^{2}+y^{2}+z^{2}+2 \left( xy+xz+yz \right) &= 16 \\ \left( x+y+z \right)^{2} &= 16 \\ x+y+z &= 4 \\ \hline z^{2}+zx+zy &= 9 \\ z \left( z+ x+ y \right) &= 9 \\ z \left( 4 \right) &= 9 \\ z &= \dfrac{9}{4} \end{align} $
$\therefore$ Pilihan yang sesuai adalah $(D)\ \dfrac{9}{4}$
39. Soal UM UGM 2019 Kode 934 |
Grafik fungsi kuadrat $y=ax^{2}+bx+c$ mempunyai puncak di $(1,1)$ dan menyinggung garis $y=x+1$. Nilai $8a-4b=\cdots$
$\begin{align} (A)\ & -4 \\ (B)\ & -2 \\ (C)\ & 0 \\ (D)\ & 2 \\ (E)\ & 4
\end{align}$
Show
Dari fungsi kuadrat $y=ax^{2}+bx+c$ dimana titik puncaknya $( 1,1)$ dan menyinggung garis $y=x+1$ dapat kita peroleh:
- Titik puncaknya $( 1,1)$
$\begin{align} x_{p} &= -\dfrac{b}{2a} \\ 1 &= -\dfrac{b}{2a} \\ -2a &= b \\ \hline y_{p} &= -\dfrac{D}{4a} \\ 1 &= -\dfrac{b^{2}-4ac}{4a} \\ -4a &= b^{2}-4ac \\ -4a &= (-2a)^{2}-4ac \\ -4a &= 4a^{2}-4ac \\ -1 &= a-c \end{align}$ - Fungsi kuadrat $y=ax^{2}+bx+c$ menyinggung garis $y=x+1$ sehingga:
$\begin{align} y &= y \\ ax^{2}+bx+c &= x+1 \\ ax^{2}+bx-x+c-1 &= 0 \\ ax^{2}+ \left(b -1 \right)x+c-1 &= 0 \\ \hline D &=0 \\ b^{2}-4ac & =0 \\ \left(b -1 \right)^{2}-4a\left(c -1 \right) & =0 \\ \left(-2a -1 \right)^{2}-4a\left( a \right) & =0 \\ 4a^{2}+4a+1-4a^{2} & =0 \\ 4a+1 & =0 \\ 4a & = -1\ \longrightarrow a=-\dfrac{1}{4} \\ \hline b & = -2a \\ b & = -2 \left( -\dfrac{1}{4} \right)= \dfrac{1}{2} \end{align}$ - Nilai $8a-4b$ adalah $8\left( -\dfrac{1}{4} \right) -4\left( \dfrac{1}{2} \right)=-4$
$\therefore$ Pilihan yang sesuai $(A)\ -4$






Posting Komentar untuk "Materi, Contoh Soal & Pembahasan Sistem Persamaan Linear Kuadrat (SPLK)"