Graphs of Trigonometric Functions

Graphs of Trigonometric Functions

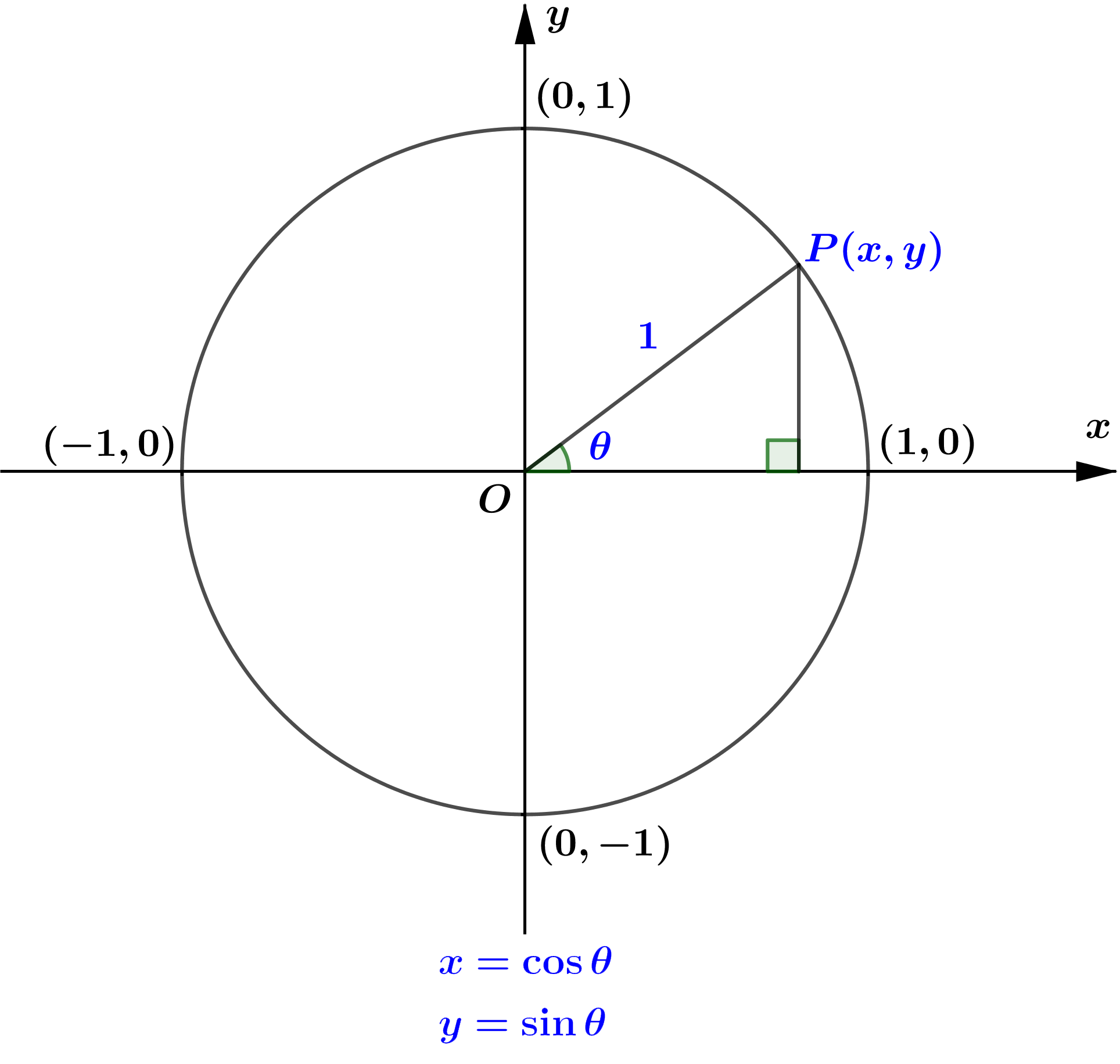
$OP$ နှင့် positive $x$-axis ကြားရှိထောင့် $(\theta)$ cosine ratio $(\cos \theta)$ သည် $OP$ နှင့် unit circle ဖြတ်သွားသော
အမှတ် $P(x,y)$ ၏ $x$-coordinate တန်ဖိုးဖြစ်ပြီး sine ratio $(\sin \theta)$ သည် $y$-coordinate တန်ဖိုးဖြစ်ကြောင်း
သိရှိခဲ့ပြီး ဖြစ်သည်။

အဆိုပါ $\sin \theta$ နှင့် $\cos \theta$ သည် $\theta$ ပေါ်မူတည်၍ပြောင်းလဲနေမည် ဖြစ်သည်ကို unit circle တွင် အလွယ်တကူ
သိရှိနိုင်သည်။ $OP$ တစ်ပတ်လှည့်ပတ်ခြင်း $ 0^{\circ} \le \theta \le 360^{\circ}$ တွင် $\sin \theta$ နှင့် $\cos \theta$ သည်
$\theta$ ပေါ်မူတည်၍ပြောင်းလဲ နေသော်လည်း တစ်ပတ်ပြည့်ပြီးနောက် နောက်တွင် မူလတစ်ပတ်က တန်ဖိုးများကိုသာ ပြန်လည်ရောက်ရှိလာမည်
ဖြစ်သည်။ ထို့သို့ တစ်ပတ်ပြည့်တိုင်း တန်ဖိုးတူနေရာများသို့ ပြန်လည်ရောက်ရှိလာသော $\sin \theta$ နှင့် $\cos \theta$ တို့ကို periodic
function များဟုခေါပြီး မတူညီသော တန်ဖိုးများ ရရှိစေသည့် တစ်ပတ် $360^{\circ} \text{or } 2\pi$ ကို $\sin \theta$ နှင့် $\cos \theta$
တို့၏ period ဟုခေါ်သည်။

unit circle ၏ အဝန်းပိုင်းကို $(1,0)$ နေရာမှ ဖြတ်တောက်၍ အဖြောင့်အတိုင်းထားလိုက်သည်ဟု ယူဆမည်။
အဝန်းပိုင်းပေါ်ရှိ $\theta$ ၏ တန်ဖိုးနှင့် သက်ဆိုင်ရာ Trigonometric
function value ၏ တန်ဖိုးများကို နှိုင်းယှဉ်ဖော်ပြခြင်းဖြင့် သတ်မှတ်ထာသော Trigonometric Function ၏ graph ကို
ရရှိမည်ဖြစ်သည်။ အောက်ပါ applet တွင် trigonometric function တစ်ခုချင်းစီ၏ $0 \le \theta \le 2\pi$ အတွင်း
ရရှိလာမည့် trigonometric graph တစ်ခုစီကို လေ့လာနိုင်ပါသည်။

The Graph of $\ { y=\sin\theta}$

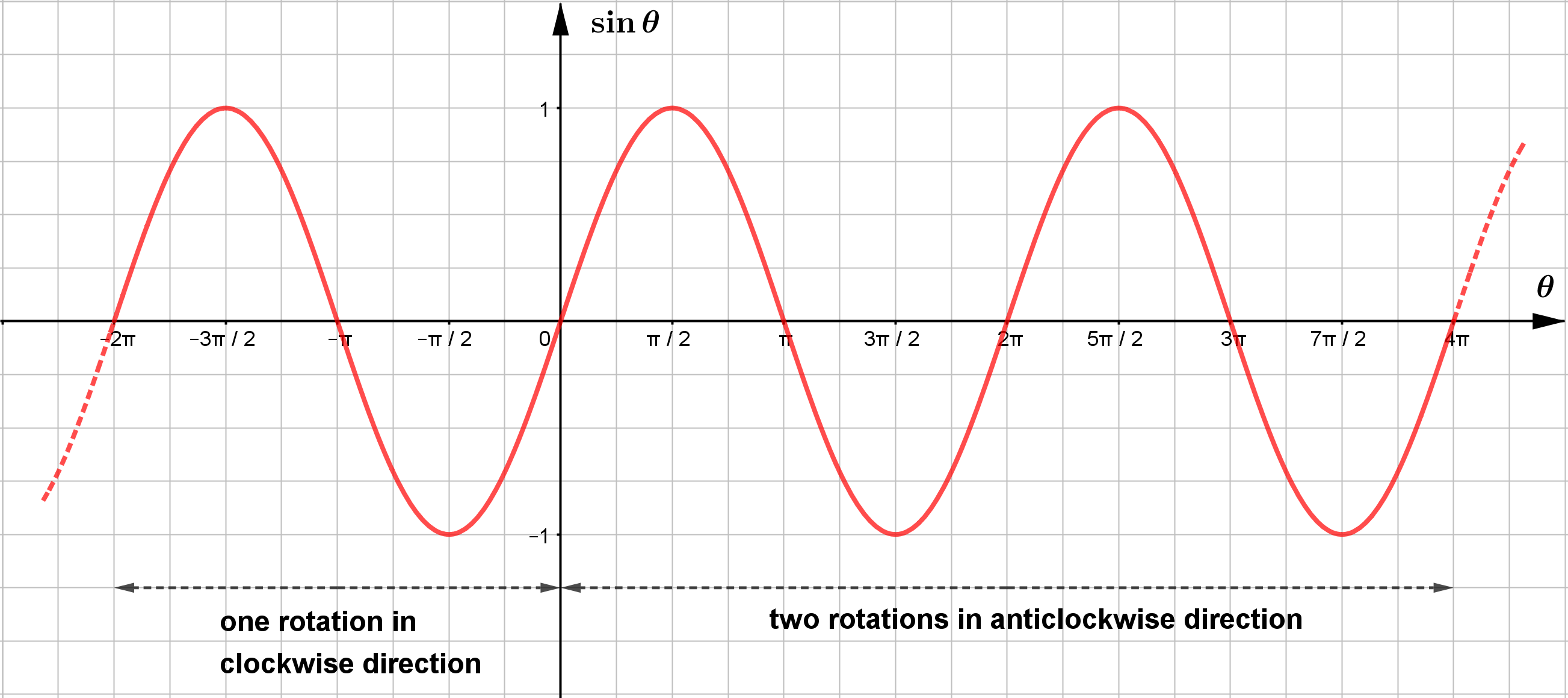
terminal side ကို aticlockwise direction ဖြင့် လှည့်သည့်အခါ $\sin \theta$ ၏ graph သည် positive $x$-axis
ဘက်တွက် တစ်ပတ်ပြည့်တိုင်း wave တစ်ခု ဖြစ်လာပြီး clockwise direction ဖြင့် လှည့်သည့်အခါ $\sin \theta$ ၏ graph
သည် negative $x$-axis ဘက်တွက် တစ်ပတ်ပြည့်တိုင်း wave တစ်ခု ဖြစ်လာမည်ဖြစ်သည်။ ထို့ကြောင့် $y=\sin\theta$ ၏
graph ကို sine wave (သို့) sinusoidal wave ဟုလည်းခေါ်သည်။ sine wave တစ်ခု ဖြစ်ရန်လိုအပ်သော $\theta$ တန်ဖိုးကို
period ဟုခေါ်သည်။ ထို့ကြောင့် $y=\sin\theta$ ၏ period သည် $360^{\circ} \text{or } 2\pi$ ဖြစ်သည်။

$y=\sin\theta$ ၏ maximum value သည် $1$ ဖြစ်ပြီး minimum value သည် $-1$ ဖြစ်သည်။ ထို့ကြောင့် မည်သည့် $\theta$
တန်ဖိုးအတွက် မဆို $-1\le \sin\theta\le 1$ ဖြစ်သည်။ အဆိုပါကြားပိုင်းကို sine function ၏ range ဟု ခေါ်သည်။ $y=\sin\theta$ သည်
wave ရွေ့လျားရာမျဉ်း (line of propagation) မှ အမြင့်ဆုံးအမှတ်ထိ $1$ unit ရှိပြီး အနိမ့်ဆုံးအမှတ်သို့လည်း $1$ unit ရှိသည်။
ထို့သို့ line of propagation မှ အမြင့်ဆုံးအမှတ် (သို့မဟုတ်) line of propagation မှ အနိမ့်ဆုံးအမှတ် သို့ အကွာအဝေးကို amplitude
ဟုခေါ်သည်။ အခြားတစ်နည်းဆိုရသော် အမြင့်ဆုံးအမှတ် နှင့် အနိမ့်ဆုံးအမှတ် နှစ်ခုကြား အကွာအဝေး၏ တစ်ဝက်ကို amplidude ဟု ခေါ်နိုင်သည်။

The Graph of $\ { y=a\sin\theta}$

$y=\sin\theta$ တွင် $-1\le \sin\theta\le 1$ ဖြစ်သောကြောင့် $y=a\sin\theta$
တွင် $-a\le a\sin\theta\le a$ ဖြစ်မည်။ ထို့ကြောင့် ...

The amplitude of $\ y=a\sin\theta\ $ is $a$ units


ဟုမှတ်သားနိုင်သည်။

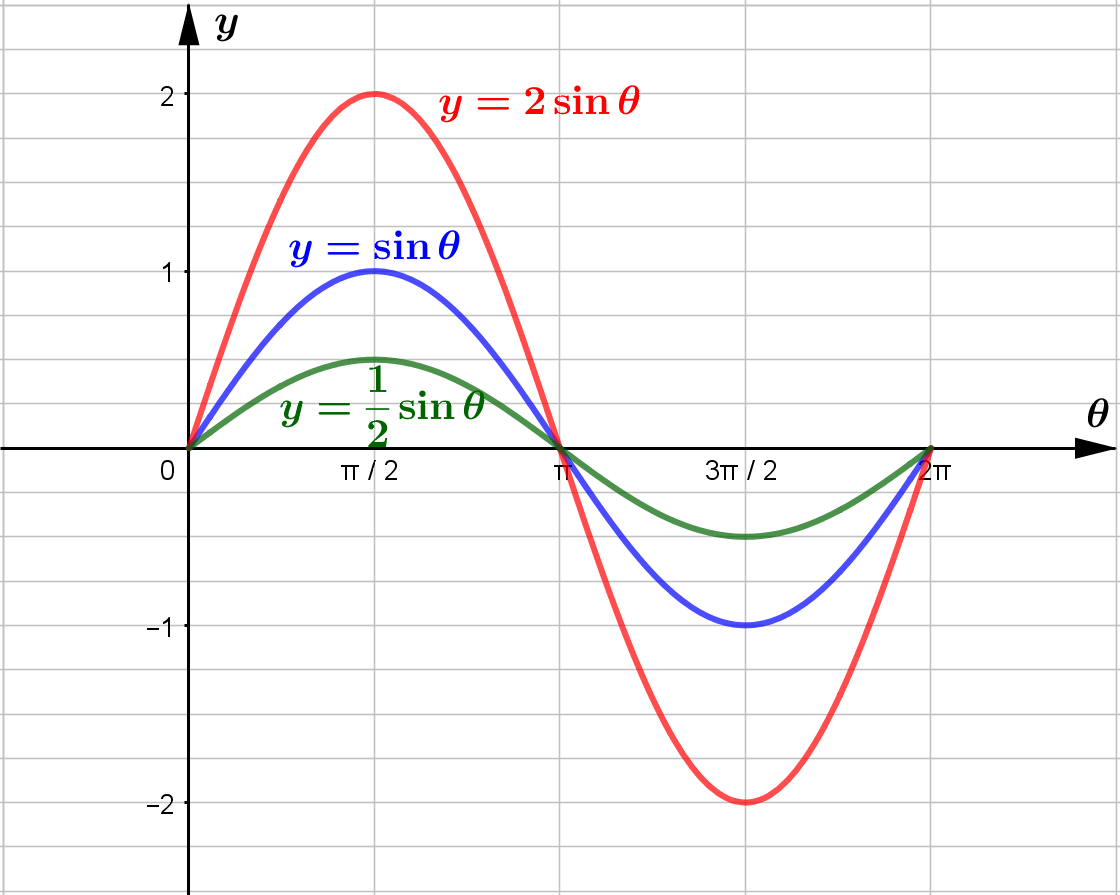
ထို့ကြောင့် ...



$y=\sin\theta\Rightarrow$ amplitude $=1$



$y=2\sin\theta\Rightarrow$ amplitude $=2$



$y=\displaystyle\frac{1}{2}\sin\theta\Rightarrow$ amplitude $=\displaystyle\frac{1}{2}$

Grade 11 တွင် လေ့လာခဲ့ပြီးဖြစ်သော Trasformation ရှုထောင့်မှကြည့်လျှင် $y=a\sin\theta$ သည် $y=\sin\theta$ ကို
vertical scaling ပြုလုပ်လိုက်ခြင်း ဖြစ်ပြီး scale factor $=a$ ဖြစ်သည်ဟု မှတ်သားနိုင်သည်။ ထို့ကြောင့် $y=\sin\theta$ ကို
vertical scaling ပြုလုပ်လျှင် scale factor သည် amplitude ဖြစ်သည်။

The Graph of $\ { y=\sin(b\cdot\theta})$

ဆက်လက်၍ အောက်ပါ diagram ကို လေ့လာကြည့်ပါ။

period of $y=\sin\theta\Rightarrow 2\pi$

$y=\sin 2\theta $ သည် $y=\sin \theta $ ကို horizontal scaling ပြုလုပ်လိုက်ခြင်း ဖြစ်ပြီး scale factor မှာ
$\displaystyle\frac{1}{2}$ ဖြစ်သည်။ $y=\sin 2\theta $ ၏ period (the value of $\theta$ to form one complete cycle)
မှာ $\pi$ ဖြစ်သည်ကို တွေ့ရမည်။


အလားတူပင် $y=\sin \displaystyle\frac{1}{2}\theta $ သည် $y=\sin \theta $ ကို horizontal scaling ပြုလုပ်လိုက်ခြင်း ဖြစ်ပြီး
scale factor မှာ $2$ ဖြစ်သည်။ $y=\sin \displaystyle\frac{1}{2}\theta $ ၏ period မှာ $4\pi$ ဖြစ်သည်။

ထို့ကြောင့် $y=\sin \theta $ ကို horizontal scaling ပြုလုပ်လိုက်ခြင်းဖြင့် period ကို အပြောင်းအလဲ ဖြစ်စေပြီး
ပြောင်းလဲသွားသော period တန်ဖိုးမှာ scale factor $\times 2\pi\ $ ဖြစ်သည်ကို တွေ့ရမည်။
အောက်ပါအတိုင်း ယျေဘုယျ မှတ်သားနိုင်ပါသည်။

$\begin{array}{|l|}
\hline
\text{For the function } y=a \sin(b\cdot \theta)\\\\
\text{amplitude } = a \text{ units}\\\\
\text{ period } = \displaystyle\frac{2\pi}{b}\\
\hline
\end{array}$

The Graph of $\ y=a\sin\left(b\cdot\theta + c\right)+d$

Grade 11 တွင် လေ့လာခဲ့ပြီးဖြစ်သော Function Transformation ၏ rule များအတိုင်း
$\ y=a\sin\left(b\cdot\theta + c\right)+d$
တွင် $c$ သည် $y=\sin\theta$ ကို horizontal translation ပြုလုပ်ပေးခြင်း ဖြစ်ပြီး $d$ သည် $y=\sin\theta$ ကို
vertical translation ပြုလုပ်ပေးခြင်း ဖြစ်သည်ဟု သိရှိရမည် ဖြစ်သည်။

ဥပမာ အနေဖြင့် $y=\sin\theta$ နှင့် $y=\displaystyle\frac{3}{2}\sin\left(2\theta-\frac{\pi}{3}\right)$ တို့ကို
နှိုင်းယှဉ်လေ့လာကြည့်ပါမည်။



For $y=\sin\theta$,



period = $2\pi$



amplitude = $1$



$\begin{array}{|c|c|c|c|c|c|}
\hline
x & 0 & \displaystyle\frac{\pi}{2} & \pi & \displaystyle\frac{3\pi}{2} & 2\pi\\
\hline
y & 0 & 1 & 0 & -1 & 0\\
\hline
\end{array}$



For $y=\displaystyle\frac{3}{2}\sin\left(2\theta-\frac{\pi}{3}\right)$,



period = $\frac{1}{2}\times2\pi=\pi$



amplitude = $\displaystyle\frac{3}{2}$



Let $f(\theta)=\sin\theta$ then $y=\displaystyle\frac{3}{2}\sin\left(2\theta-\frac{\pi}{3}\right)
=\displaystyle\frac{3}{2}f\left(2\theta-\frac{\pi}{3}\right)$.



အထက်ပါ ဇယားတွင် ဖော်ပြထားသော $y=\sin\theta$ ပေါ်တွင်ရှိသော အမှတ်များ ၏
$y=\displaystyle\frac{3}{2}\sin\left(2\theta-\frac{\pi}{3}\right)$ ပေါ်တွင်ရှိသော mapped point များကို
transformation method ဖြင့်ရှာကြည့်ပါမည်။



$\begin{array}{l}
\displaystyle(0,0)\xrightarrow{f\left(\theta-\frac{\pi}{3}\right)}\left(\frac{\pi}{3},0\right)\\
\hspace{1.3cm}\displaystyle\xrightarrow{f\left(2\theta-\frac{\pi}{3}\right)}\left(\frac{\pi}{6},0\right)\\
\hspace{1.3cm}\displaystyle\xrightarrow{\frac{3}{2}f\left(2\theta-\frac{\pi}{3}\right)}\left(\frac{\pi}{6},0\right)\\
\end{array}$



$\begin{array}{l}
\displaystyle(\frac{\pi}{2},1)\xrightarrow{f\left(\theta-\frac{\pi}{3}\right)}\left(\frac{5\pi}{6},1\right)\\
\hspace{1.3cm}\displaystyle\xrightarrow{f\left(2\theta-\frac{\pi}{3}\right)}\left(\frac{5\pi}{12},1\right)\\
\hspace{1.3cm}\displaystyle\xrightarrow{\frac{3}{2}f\left(2\theta-\frac{\pi}{3}\right)}\left(\frac{5\pi}{12},\frac{3}{2}\right)\\
\end{array}$



$\begin{array}{l}
\displaystyle(\pi,0)\xrightarrow{f\left(\theta-\frac{\pi}{3}\right)}\left(\frac{4\pi}{3},0\right)\\
\hspace{1.3cm}\displaystyle\xrightarrow{f\left(2\theta-\frac{\pi}{3}\right)}\left(\frac{2\pi}{3},0\right)\\
\hspace{1.3cm}\displaystyle\xrightarrow{\frac{3}{2}f\left(2\theta-\frac{\pi}{3}\right)}\left(\frac{2\pi}{3},0\right)\\
\end{array}$




$\begin{array}{l}
\displaystyle(\frac{3\pi}{2},-1)\xrightarrow{f\left(\theta-\frac{\pi}{3}\right)}\left(\frac{11\pi}{6},-1\right)\\
\hspace{1.3cm}\displaystyle\xrightarrow{f\left(2\theta-\frac{\pi}{3}\right)}\left(\frac{11\pi}{12},-1\right)\\
\hspace{1.3cm}\displaystyle\xrightarrow{\frac{3}{2}f\left(2\theta-\frac{\pi}{3}\right)}\left(\frac{11\pi}{12},-\frac{3}{2}\right)\\
\end{array}$



$\begin{array}{l}
\displaystyle(2\pi,0)\xrightarrow{f\left(\theta-\frac{\pi}{3}\right)}\left(\frac{7\pi}{3},0\right)\\
\hspace{1.3cm}\displaystyle\xrightarrow{f\left(2\theta-\frac{\pi}{3}\right)}\left(\frac{7\pi}{6},0\right)\\
\hspace{1.3cm}\displaystyle\xrightarrow{\frac{3}{2}f\left(2\theta-\frac{\pi}{3}\right)}\left(\frac{7\pi}{6},0\right)\\
\end{array}$



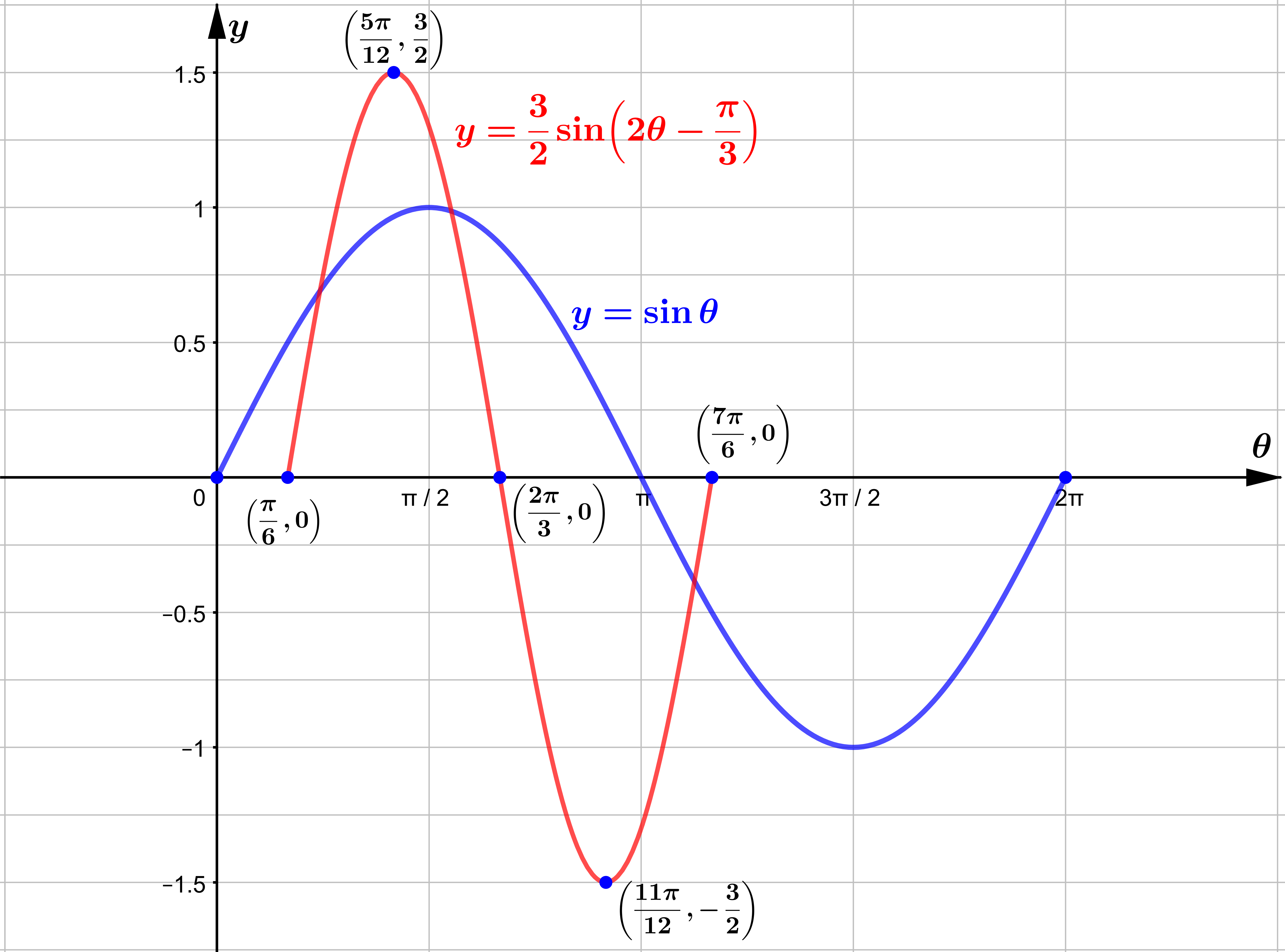
ထို့ကြောင့် $y=\sin\theta$ နှင့် $y=\displaystyle\frac{3}{2}\sin\left(2\theta-\frac{\pi}{3}\right)$ တို့၏
graph နှစ်ခုကို sketch လုပ်နိုင်ပြီဖြစ်ရာ အောက်ပါအတိုင်း ရရှိမည်ဖြစ်သည်။

The Graph of $\ y=\cos\theta $

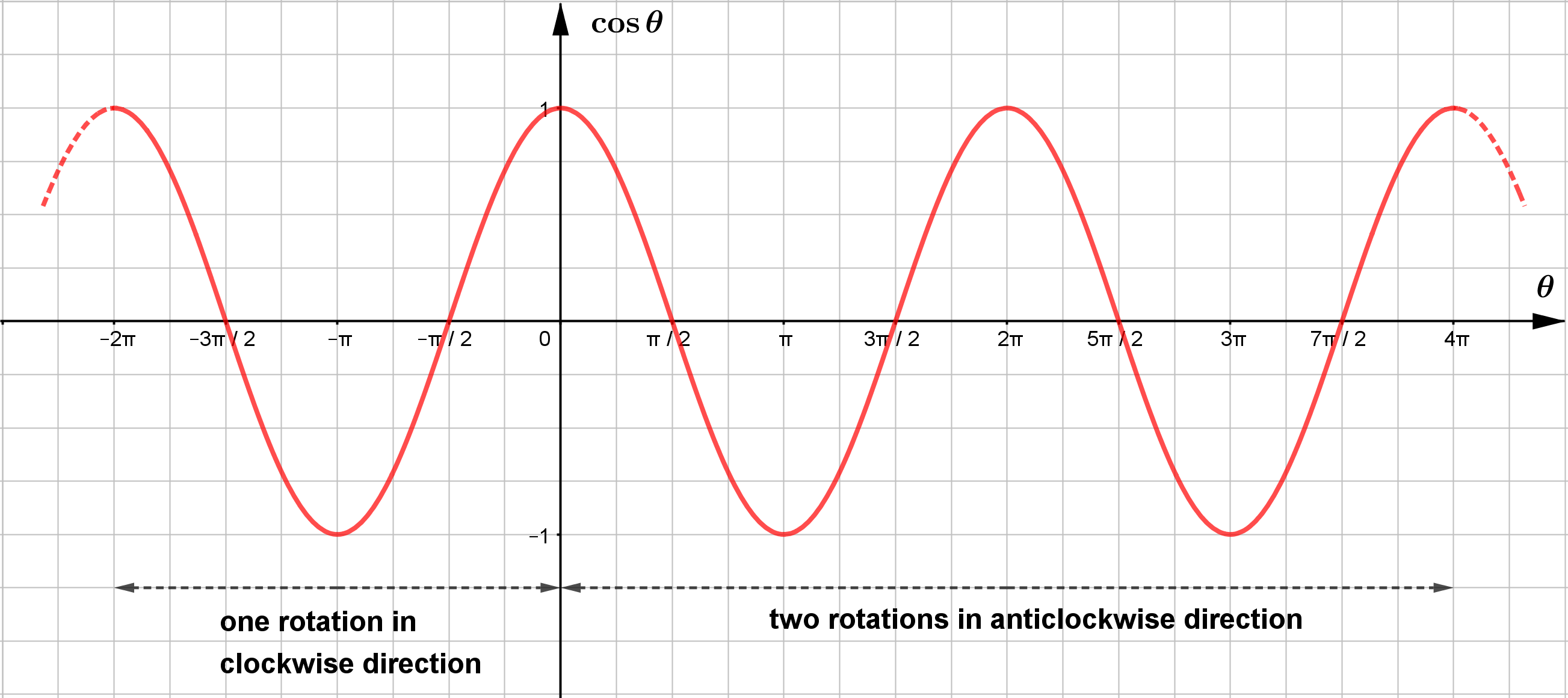
$\ y=\cos\theta $ ၏ graph သည် လည်း sine wave ကဲ့သို့ပင် one complete cycle ဖြစ်ရန်
$\theta=360^{\circ} = 2\pi$ ဖြစ်သည်။ ထို့ကြောင့် $\ y=\cos\theta $ ၏ period မှာ $2\pi$ ဖြစ်မည်။
$\ y=\sin\theta $ ကဲ့သို့ပင် $\ y=\cos\theta $ ၏ range သည်လည်း $-1\le\cos\theta\le 1 $ ဖြစ်ရာ
amplitude မှာ 1 iunit ဖြစ်သည်။

$\displaystyle\sin \left(\frac{\pi}{2}-\theta=\cos\theta\right)$ ဟု သိရှိခဲ့ပြီးဖြစ်သည်။



$y=\cos\theta$ သည် $y=\sin\theta$ ကို horizontal translation ပြုလုပ်ထားခြင်းပင်ဖြစ်သည်။



ထို့ကြောင့် $y=\cos\theta$ သည် $y=\sin\theta$ ၏ ဂုဏ်သတ္တိများနှင့် တူညီသည်။



sine function နှင့်
cosine function များ၏ ဂုဏ်သတ္တိများကို အောက်ပါ အတိုင်းအချုပ်မှတ်နိုင်သည်။

Functions	Amplitude	Period	Range
$y=\sin\theta$	1	$2\pi$	$-1\le\sin\theta\le 1$
$y=a(b\cdot \sin\theta+c)+d$	a	$\displaystyle\frac{2\pi}{b}$	$-a+d\le a(b\cdot \sin\theta+c)+d\le a+d$
$y=\cos\theta$	1	$2\pi$	$-1\le\sin\theta\le 1$
$y=a(b\cdot \cos\theta+c)+d$	a	$\displaystyle\frac{2\pi}{b}$	$-a+d\le a(b\cdot \cos\theta+c)+d\le a+d$

Question 1

Figure 1

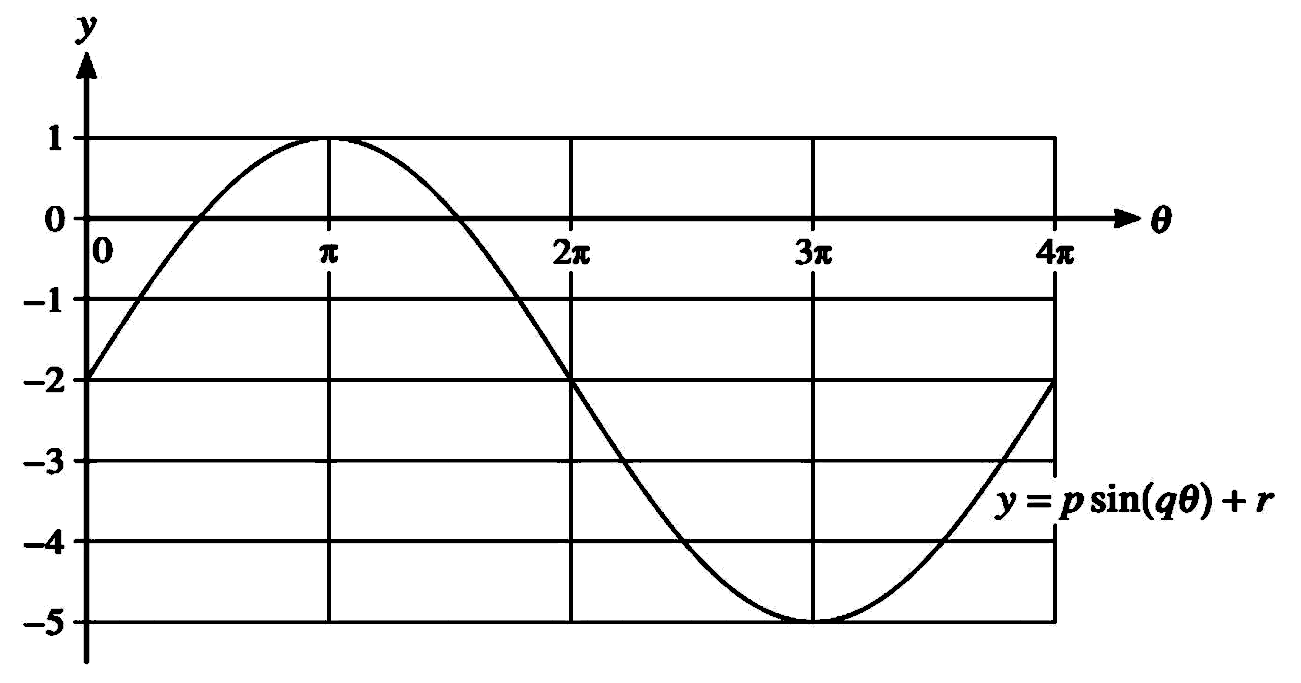
The diagram shows part of the curve with equation
$y=p \sin (q \theta)+r$, where $p, q$ and $r$ are constants.
























(a) State the value of $p$.


(b) State the value of $q$.


(c) State the value of $r$.



SOLUTION
$\begin{aligned}
& y=p \sin (q \theta)+r \\\\
\therefore \quad & \text { amplitude }=p \\\\
& \text { period }=\frac{2 \pi}{q} \\\\
& \text { From diagram, we have } \\\\
& p=3 \\\\
& \frac{2 \pi}{q}=4 \pi \Rightarrow q=\frac{1}{2} \\\\
& f(0)=-2 \\\\
& p \sin 0+r=-2 \Rightarrow r=-2
\end{aligned}$

Question 2

Figure 2

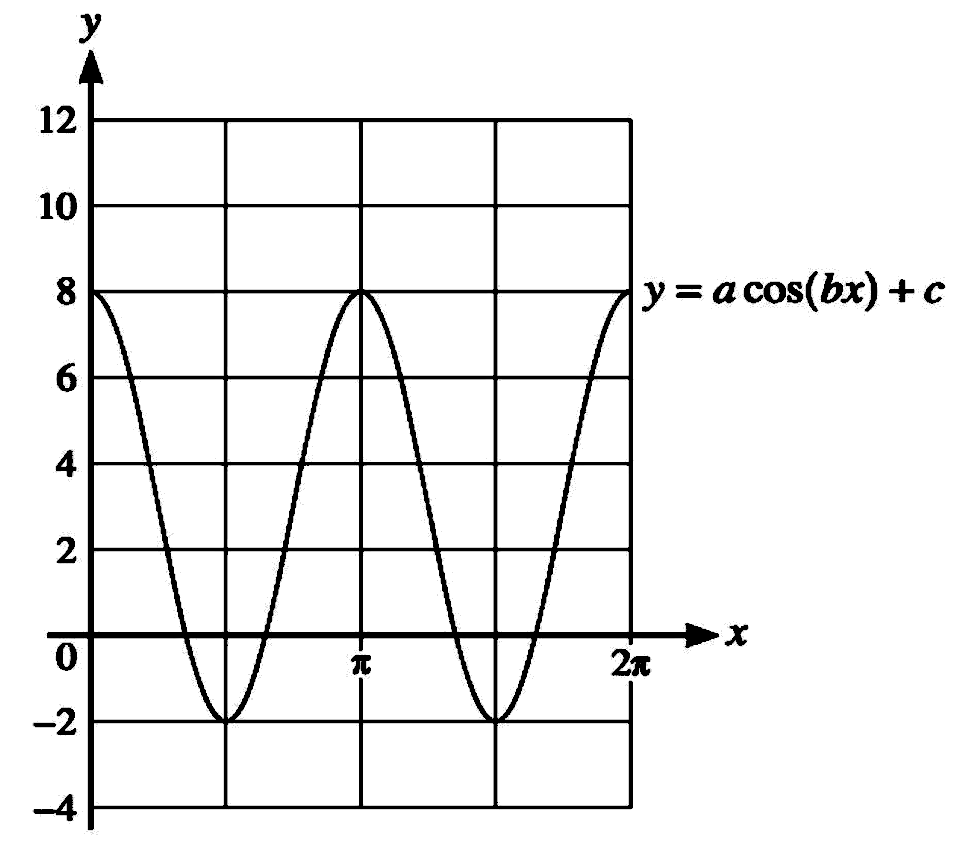
The diagram shows part of the graph of $y=a \cos (b x)+c$.


(a) Find the values of the positive integers $a, b$ and $c$.


(b) For these values of $a, b$ and $c$, use the given diagram to determine
the number of solutions in the interval $0 \leqslant x \leqslant 2 \pi$ for
each of the following equations.


(i) $\displaystyle a \cos (b x)+c=\frac{6}{\pi} x$


(ii) $\displaystyle a \cos (b x)+c=6-\frac{6}{\pi} x$.

SOLUTION


$\begin{aligned}
& y=a \cos (b x)+c \\\\
\therefore\quad & \text { amplitude }=a \\\\
& \text { period }=\frac{2 \pi}{b} \\\\
& \text { By the diagram, } \\\\
& a=\frac{8+2}{2}=5 \\\\
& \frac{2 \pi}{b}=\pi \Rightarrow b=2.\\\\
& f(0)=8 \\\\
& 5 \cos (0)+c=8 \\\\
& 5+c=8 \\\\
& c=3 .
\end{aligned}$




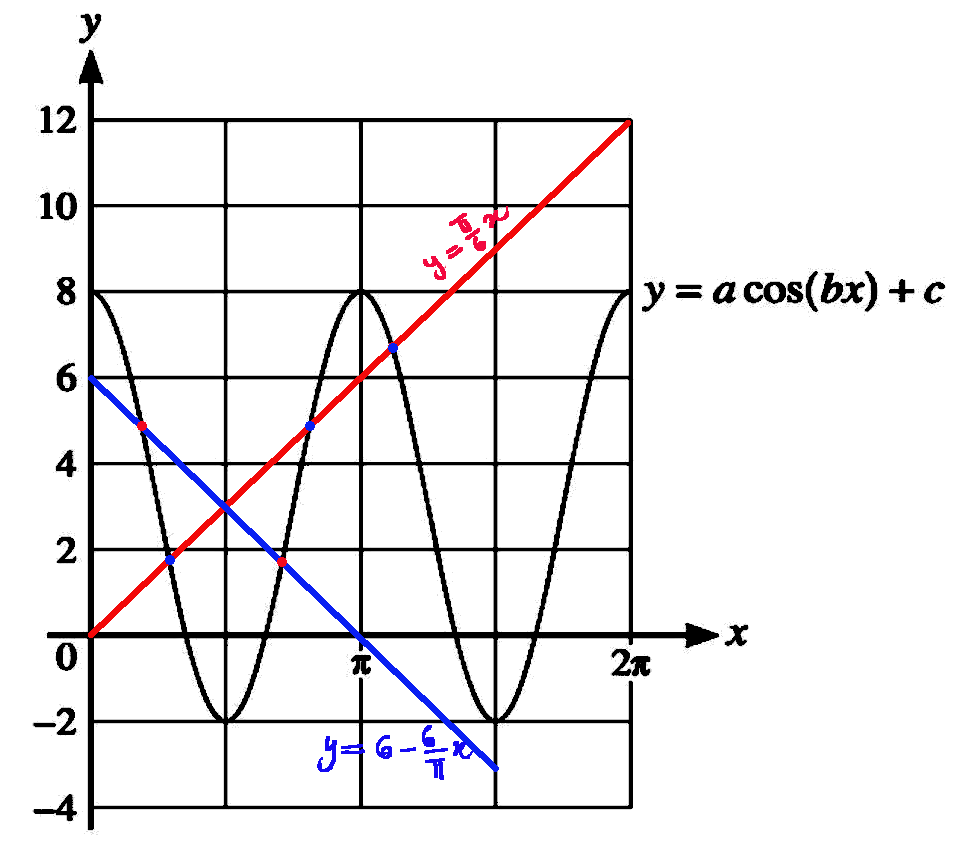
For the graph $y=\displaystyle\frac{6}{\pi} x$


$\begin{array}{|l|l|l|}
\hline x & 0 & 2 \pi \\
\hline y & 0 & 12 \\
\hline
\end{array}$


The sohtions those satisfy the equation $a \cos (b x)+c=\displaystyle\frac{5}{\pi} x$
are the points of intersection of $y=a \cos (b x)+c$ and $y=\displaystyle\frac{6}{\pi} x$.



By the diagrams, three ane 3 solutions.



For the graph $y=6-\frac{6}{\pi} x$



$\begin{array}{|c|c|c|}
\hline x & 0 & \displaystyle\frac{3 \pi}{2} \\
\hline y & 6 & -3 \\
\hline
\end{array}$



$y=a \cos (b x)+c$ intersects $y=6-\displaystyle\frac{6}{\pi} x$ at two points.


Hence there are two solutions.

Question 3

Figure 3

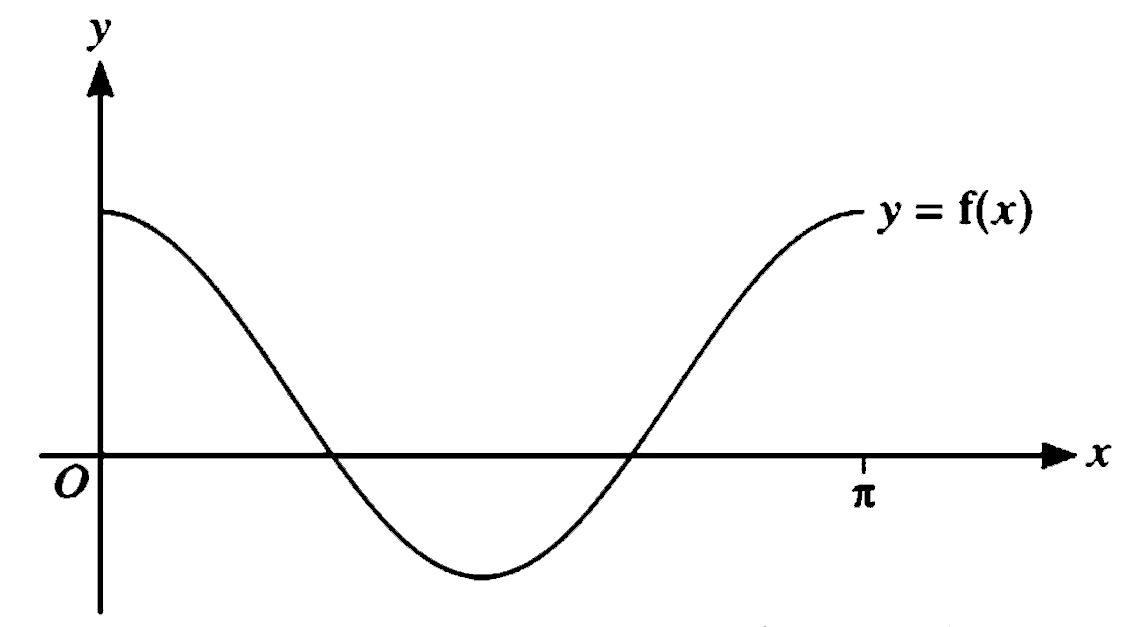
The diagram shows the graph of $y=f(x)$, where $f(x)=\displaystyle\frac{3}{2} \cos 2 x+\frac{1}{2}$
for $0 \leqslant x \leqslant \pi$.



(a) State the range of $f$.



A function $g$ is such that $g(x)=f(x)+k$, where $k$ is a positive constant.
The $x$-axis is a tangent to the curve $y=g(x)$.



(b) State the value of $k$ and hence describe fully the transformation that maps
the curve $y=f(x)$ on to $y=g(x)$.

SOLUTION
$\begin{aligned}
& f(x)=\displaystyle\frac{3}{2} \cos 2 x+\displaystyle\frac{1}{2}, 0 \leq x \leq \pi \\\\
\therefore & -\displaystyle\frac{3}{2}+\displaystyle\frac{1}{2} \leq t \leq \displaystyle\frac{3}{2}+\displaystyle\frac{1}{2} \\\\
\therefore & -1 \leq f \leq 2 . \\\\
& g(x)=f(x)+k
\end{aligned}$



This means that $g(x)$ is obtained from translating $f(x)\ \ k$ units vertically.


The $x$.axis tangent to $y=g(x)$.




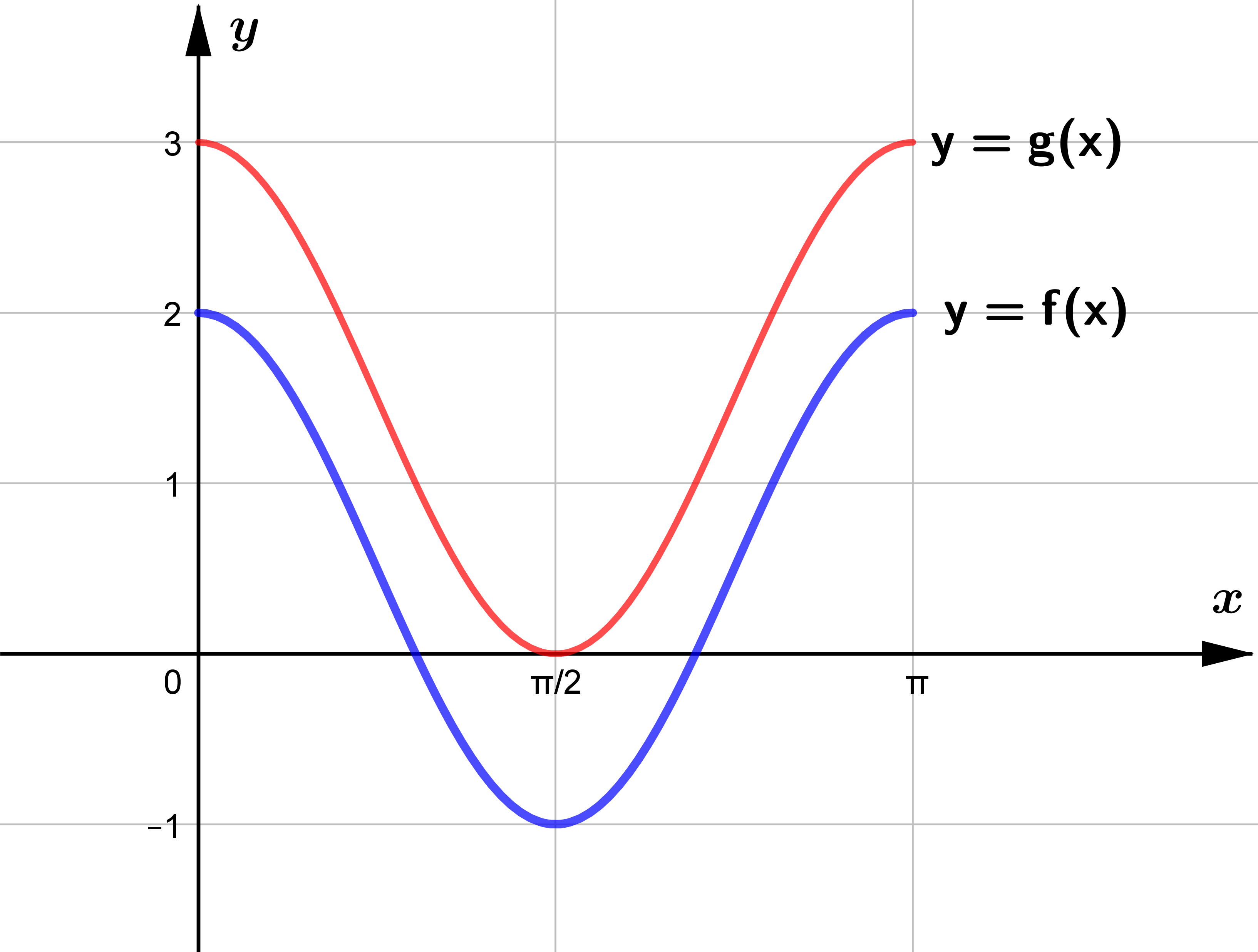
$\therefore\quad k=1$



$\therefore g(x)$ is obtained by vertical translation of $f(x)$ one unit upward.

Berbagi